Many tech workers think of themselves as edgy, as outsiders, as countercultural, even as they’re part of immense corporations that dominate culture, politics and the economy.
(Rebecca Solnit, “In the Shadow of Silicon Valley,” London Review of Books, February 8, 2024)
It was a privilege for me to work as one of the guest editors1 of the special issues of the Bulletin of the American Mathematical Society — both of them — devoted to “wonder[ing]… what the potential impact of AI will be on how we do mathematics,” in the words of Bulletin chief editor Alejandro Adem, and more generally on the question “Will machines change mathematics?” I am deeply grateful to Akshay Venkatesh for having initiated the reflection with his article in the first special issue (already reviewed here); to the Fields Institute for having hosted the Fields Medal Symposium that brought together many of the special issues’ authors; to the AMS Bulletin for having agreed to devote two special issues to the topic; and to Andrew Granville who led the team of guest editors and guaranteed that authors would get their material in on time and editors would make sure that every article was comprehensively reviewed and discussed.
This week and the next I’m busy with conferences and do not have time to write original material, so I am taking this opportunity to encourage readers to read the two special issues, cover to cover if possible. To this end I will be quoting extensively from a few of the articles below. About half of them were written by full-time mathematicians, with a few more written by computer scientists. The authors also include three philosophers and an anthropologist, and several who don’t easily fit within traditional disciplinary boundaries. It’s fairly safe to say that this is the first time in many years (or ever?)2 that so many perspectives have been collected in one place on an issue of such immediate importance to mathematics.
One can read most of the articles, however, and come away with the impression that, if machines will indeed change mathematics, they will do it on their own; the human processes — and, more specifically, the corporate processes — that will be needed to bring about these changes are largely overlooked. Many of the articles include more or less extended variants of Eugenia Cheng’s prosopopoeial3 sentence
Technology has now developed further.
Michael Shulman’s article, for example, is remarkable not only for its account of the motivations for homotopy type theory as a foundational theory but also for his optimistic vision of a future mathematics that incorporates the technology:
in addition to making today’s mathematics easier, faster, and more reliable, I believe the enhanced proof assistants of the future may enable us to achieve new results and understandings that would previously have been prohibitively difficult.
His article makes no predictions about the circumstances that could lead to the creation of this future; it's possible to read it and conclude that these developments will be generated entirely within the community of mathematicians, presumably in collaboration with computer scientists. An artificial intelligence of the future, reading this, is likely to assume that the “enhanced proof assistants of the future” are not only the subject of the subordinate clause that expresses Shulman’s belief but are indeed themselves the4 enablers of the process by which “we” overcome prohibitive difficulties.
This is not meant as criticism, which in any way would be directed at me, as one of the guest editors, as much as anyone else. It rather points to the challenges mathematicians face in living up to the final words of the guest editors’ two-page introduction to the special issues —
It is for us to determine how our subject should develop, and so we invite the mathematical community to think seriously about and discuss the questions raised in these two special issues, and to listen to colleagues in other fields who have deeply considered these same questions. Now is the time for mathematicians to learn about and then drive this debate, and to decide upon our subject’s future direction.
— if we persist in treating the technology as an autonomous force, rather than the effect of choices made by groups of human beings who may be steering our subject in directions we would not necessarily have chosen.
There are a few exceptions. Rodrigo Ochigame, the anthropologist, devotes several paragraphs to reminding mathematicians that the drive to mechanize mathematics has always involved forces with considerably more power than our academic departments:
I want to address the implicit assumption that the growth of automated mathematics is driven primarily by the intellectual needs or priorities of academic mathematicians. Rather, this area of research has been shaped significantly by the strategic interests of the military and corporate institutions that have funded it. As sociologist Donald MacKenzie has documented, early efforts in “formal verification” or “program proof” emerged largely out of practical concerns about computer security, with funding from the US military, particularly the National Security Agency (NSA).5 For instance, the military worried that a real computer program or operating system might not conform to its supposed mathematical model of “security”. By the early 1970s, the NSA perceived formal verification as central to computer security. Although military uses of computer-assisted proof have changed significantly in the fifty years since then, the US Air Force Office of Scientific Research (AFOSR) still sponsors research in this area under its “Information Assurance and Cybersecurity” program, mentioning “interactive and automated theorem proving” as well as “formalized mathematics” among research areas that “are expected to provide valuable insights into various cybersecurity problems”6.
In recent years, commercial firms such as Microsoft, Google, and Meta have become growing sources of investment in automated mathematics. Unlike the military, which focuses on specific problems with more predictable applications, those firms benefit from their investments in less direct ways. They invest in the automation of mathematics as part of a broader strategy of demonstrating AI capabilities in general, thus attracting public attention and capital investment. If the military tends to sponsor work on computer-assisted proofs under the rubric of “cybersecurity”, those firms have branded such work more often as “AI”, focusing lately on projects involving “deep learning” and “large language models”. Unsurprisingly, public-relations teams and corporate-sponsored researchers deploy hyperbolic language to publicize their work, for example, by framing their research as an effort to “create an automatic mathematician” (Google) or even asking sensationally, “Is human-led mathematics over?” (Meta)7. It remains to be seen whether academic mathematicians will embrace or refuse the modus operandi of hype-driven stock markets and venture capital.
Much of my own contribution, which has been reproduced in this newsletter,8 was devoted to elaborating on that last sentence of Ochigame. Both Venkatesh’s and Granville’s essays insisted, as did mine, that if machines change mathematics then mathematicians will need to work to ensure that the changes are in line with our values. Granville not only explicitly addressed how the priorities of the industry and its investors distort the public image of the technology…
There is a lot of money and publicity surrounding the subject of machine learning and some other forms of artificial intelligence, so it is perhaps not surprising that many hyped advances are either exaggerated or are easily explained in terms of well-designed algorithms and extraordinary computing power.
… he also included a warning to those tempted to count on the industry to help make mathematics more reliable:
Manufacturers rarely reveal concerns about their products (so as not to put off potential purchasers), so if there is a glitch, it is unlikely to be shared with users. Moreover, would a small mathematical error in a widely used computer chip be worth the cost of fixing for the manufacturers?
Other references to economic or industrial factors are limited to passing remarks, like this one in the middle of an article by Tomasso Poggio and Maia Fraser on the mathematical principles behind effective machine learning…
With this success came broad media attention for AI in general, widespread use by the public (e.g., in social media, search engines, and voice recognition), uptake by business and scientific professions—and also massive investment and profits in the private sector developing these tools.
… or the opening sentences of Geordie Williamson’s introduction, aimed at pure mathematicians, to what deep learning actually involves:
Over the last decade, deep learning has found countless applications throughout industry and science. However, its impact on pure mathematics has been modest.
For the most part, then, the special issues of the AMS Bulletin do not provide an analysis of the material and social forces that are driving the development of the technological contributions to a hypothetical mechanization of mathematics. Such an analysis is still indispensable if mathematicians are to take charge of the process. But of course there is a good deal of food for thought in these two issues. The remainder of this post quotes two of the articles by non-mathematicians who contributed to these special issues, in extended excerpts that provide novel perspectives on some of the questions with which Silicon Reckoner has been concerned since its inception.
Why error is indispensable (Simon DeDeo)
In day-to-day life, mental models are tuned by interaction with the world, through a process of learning and feedback; to develop our mental models, we use them to generate predictions about the world that we then compare to reality. If our model fails to predict correctly, we update it. This update is far from instantaneous: sustained model failures help direct our attention—we attend more closely to aspects of our experience that our models failed to predict, and prediction failures seem to be not only a core feature of low-level cognition but useful guides to high-level decision-making processes such as scientific exploration. The mathematical parallel is, most naturally, the use of mental models to be wrong about mathematics; without the possibility of being wrong, the mental model cannot change and the process of attention is diffused. This leads to a second dystopian fantasy, one where automated methods lead to a world in which our mental models become increasingly vague and low-resolution. [My emphasis, M. H.]
I am tempted to call DeDeo a pioneer in a discipline that is too new to have its own name, but instead I’ll say that he is an astrophysics Ph.D. who leads the Laboratory for Social Minds at the Santa Fe Institute and is an associate professor in Social and Decision Sciences at Carnegie Mellon University. He explains why he refers to losing the possibility of error in mathematics — the triumph of the disciplinary hygiene promised by the formalizers — as a “dystopian fantasy”:
Such a loss would be more than simply epistemic. It is not just that mathematicians would have more impoverished representations of what they are doing, but also that they would be deprived of particular experiences. Mathematicians may have a horror of error, but wandering into error is an unavoidable consequence of taking deliberate risks with our mental models—an experience inseparable from the act of exploring the world with curiosity.
Poincaré reserved a special place for mechanized mathematics (Colin McLarty)
There’s no better confirmation of DeDeo’s insight than the history of Poincaré’s duality theorem, as Colin McLarty’s article reminds us:
The Danish topologist Heegard immediately showed Poincaré’s statement of the [Poincaré duality] theorem was false even in very simple cases.
This theorem was so dear to Poincaré and his mistake was so terrible that he broke his virtually unbreakable rule against correcting past mistakes. He came back twice to correct this one. His second statement of the theorem was exactly right. All his attempted proofs are sketchy and more or less wrong.
The article, written by a philosopher with an unusually comprehensive knowledge of the history of mathematics and of many of its contemporary practices, is mainly devoted to elaborating on the following paradoxical interpretation of Poincaré’s thoughts on mechanization:
Poincaré saw it immediately [the relevance of machines to his work] and valued the idea precisely because machines neither have nor contribute any understanding.
McLarty explains:
A mechanizable proof guarantees that all the intuitions required for the theorem have been explicitly expressed. But Poincaré’s other point remains today as he saw in 1902: Implicit intuitions not yet fully expressed are vital to both learning and creating mathematics and they are not available to put into a machine.…
Poincaré urged mechanizable proof not as giving new theorems nor even as giving greater faith in the theorems. Poincaré declared mechanized proof a threat to research creativity and learning. But he found mechanizable proof essential to fully explicit understanding. For Poincaré, only mechanizability can guarantee that we have fully stated assumptions sufficient for the theorems.
McLarty finds in Poincaré’s writings a perspective on the specific value of formalization, and of its limitations, that contemporary enthusiasts would do well to ponder:
The take home message. A formal theory T admits arbitrarily many different informal interpretations giving T as many different meanings. A computer with T encoded on it, and able to derive formal conclusions from T, does not also know informal interpretation(s) of T. The programmers know the motivating informal interpretation(s) and thus the relevant “meaning(s)” of theorems derived in T.
Even more briefly:
Intuitions have specific, objective meaning which formalized theories lack.
There is no easy way to make sense of this last sentence, which McLarty extracts from his close reading of Poincaré but with which he clearly sympathizes. The difficulty of characterizing this specificity and objectivity, and for that matter of pinning down “meaning” in the setting of mathematics, helps explain why philosophers less sensitive than McLarty to mathematical practice are tempted to take refuge in formalized theories, which are themselves amenable to formal analysis, but which reduce mathematics to little more than DeDeo’s “dystopian fantasy.”
Along with Maia Fraser, Andrew Granville, Colin McLarty, Emily Riehl, and Akshay Venkatesh.
Readers are invited to share their answers to this question.
It can be eye-opening to read the BAMS volume, or any rhetorical claims regarding mechanization of mathematics, with a handbook of classical rhetoric on the table.
…conscious or unconscious…
Donald A. MacKenzie, Mechanizing proof: computing, risk, and trust, MIT Press, Cambridge, MA, 2001.
US Air Force Research Laboratory, Information and networks, August 2020. Jeremy Avigad’s article mentions the no less important motivation for formalized mathematics for purposes of
…software verification. Formal methods are commonly used at places like Amazon Web Services, Apple, and Facebook to verify the correctness of code.
Meta AI, Teaching AI advanced mathematical reasoning, November 2022; Markus N. Rabe and Christian Szegedy, Towards the automatic mathematician, Automated Deduction – CADE 28 (André Platzer and Geoff Sutcliffe, eds.), Springer, Cham, 2021, pp. 25–37.


That's too specific a question. But there are some people I would trust, for example the authors of the Stochastic Parrots paper.
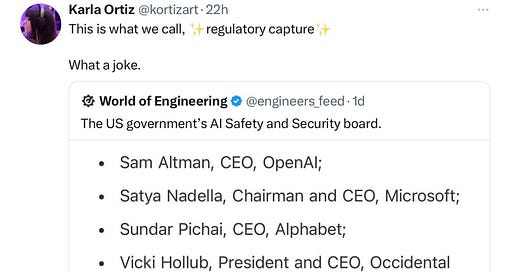
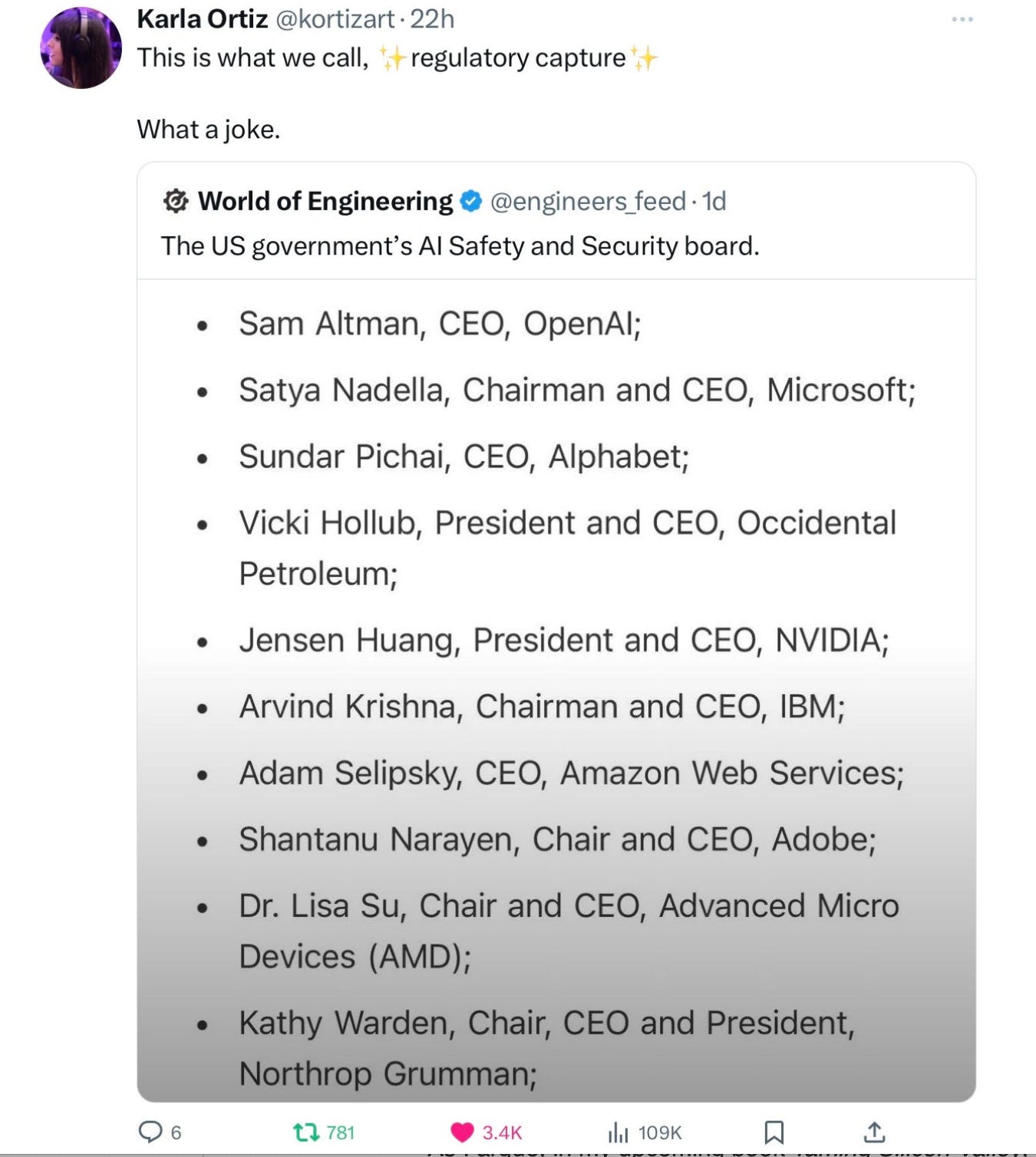
What would be your "Dream Team" of nominees (by name, say) for "The US government's AI Safety and Security board"?