Automation compels mathematicians to reflect on our values, Part II
Part II of the August 23, 2023 post entitled "In which the author harangues mathematicians…"
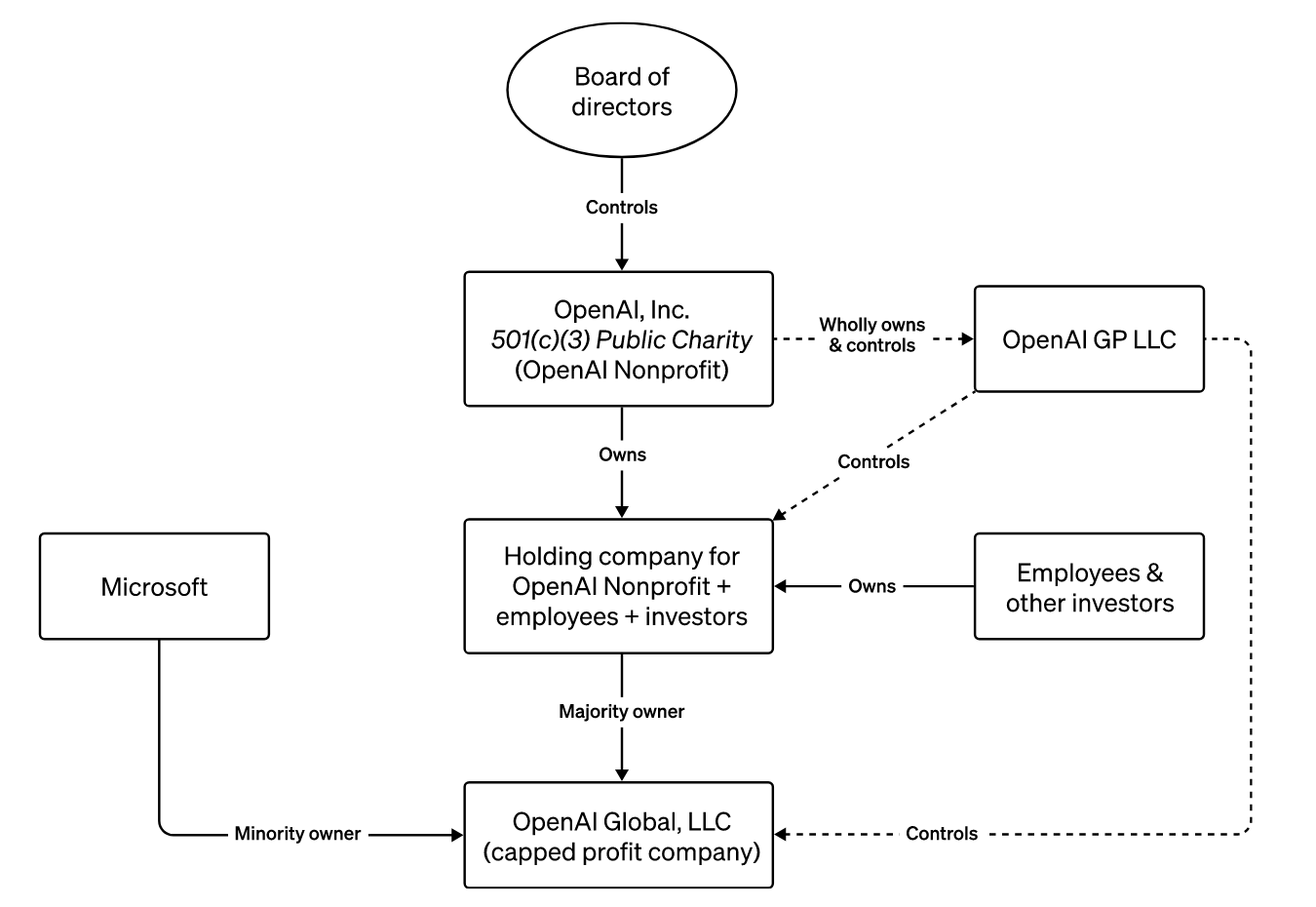
The question I'm trying to raise is bigger: what OpenAI, Anthropic, DeepMind have all tried to do is raise billions & tap vast GPU resources of tech giants without having the resulting tech de facto controlled by them. I'm arguing the OpenAI fracas show that might be impossible. (Jeremy Kahn, Tweet 11:19 AM, November 19, 2023)
Kahn is referring to his November 19 Fortune article that explains the background to Sam Altman’s firing two days earlier by the OpenAI board, followed by reports the very next day of an “outcry from his supporters and the company’s investors” that (may have) led to his reinstatement. Kahn’s article is behind a paywall but Gary Marcus quotes some of the main points in his Substack newsletter.
“OpenAI’s structure was designed to enable OpenAI to raise the tens or even hundreds of billions of dollars it would need to succeed in its mission of building artificial general intelligence (AGI), the kind of AI that is as smart or smarter than people at most cognitive tasks, while at the same time preventing capitalist forces, and in particular a single big tech giant, from controlling AGI”
“Altman … struck the deal—for just $1 billion initially—with Nadella in 2019. From that moment on, the structure was basically a time bomb. By turning to a single corporate entity, Microsoft, for the majority of the cash and computing power OpenAI needed to achieve its mission, it was essentially handling control to Microsoft, even if that control wasn’t codified in any formal governance mechanism.”
If Altman returns and the board resigns as now seems likely, “it will prove that Altman’s structure failed—OpenAI was not able to both raise billions of dollars from a big tech corporation while somehow remaining free from that corporation’s control.”
“It would be the ultimate irony if the flaws of the very structure Altman designed wind up saving his job at CEO and allowing him to outmaneuver the board that he established to safeguard AGI.”
Mathematicians may feel this story is remote from our concerns. Most of today’s post is devoted to the second half of my article for the upcoming special issue “Will Machines Change Mathematics?” (WMCM?) of the AMS Bulletin. The first half appeared last August under a long-ish provision title. The actual title is the one you see above:
Automation compels mathematicians to reflect on our values
which will be completed, the Bulletin permitting, by
The rest of the world has much to teach us
The “rest of the world” includes colleagues in the humanities and social sciences, such as those quoted in the article’s first half. It also includes journalists like Jeremy Kahn, who remind us that the race to develop AGI is ultimately about maximizing return on investment. Few of AI’s boosters among mathematicians seem willing to acknowledge that for most readers of publications like Fortune, the question WMCM? ranks very low among their priorities. The Altman melodrama is a timely reminder that it is readers of Fortune, rather than of the AMS Bulletin, who are in a position to have the last word in deciding how that question will be answered.
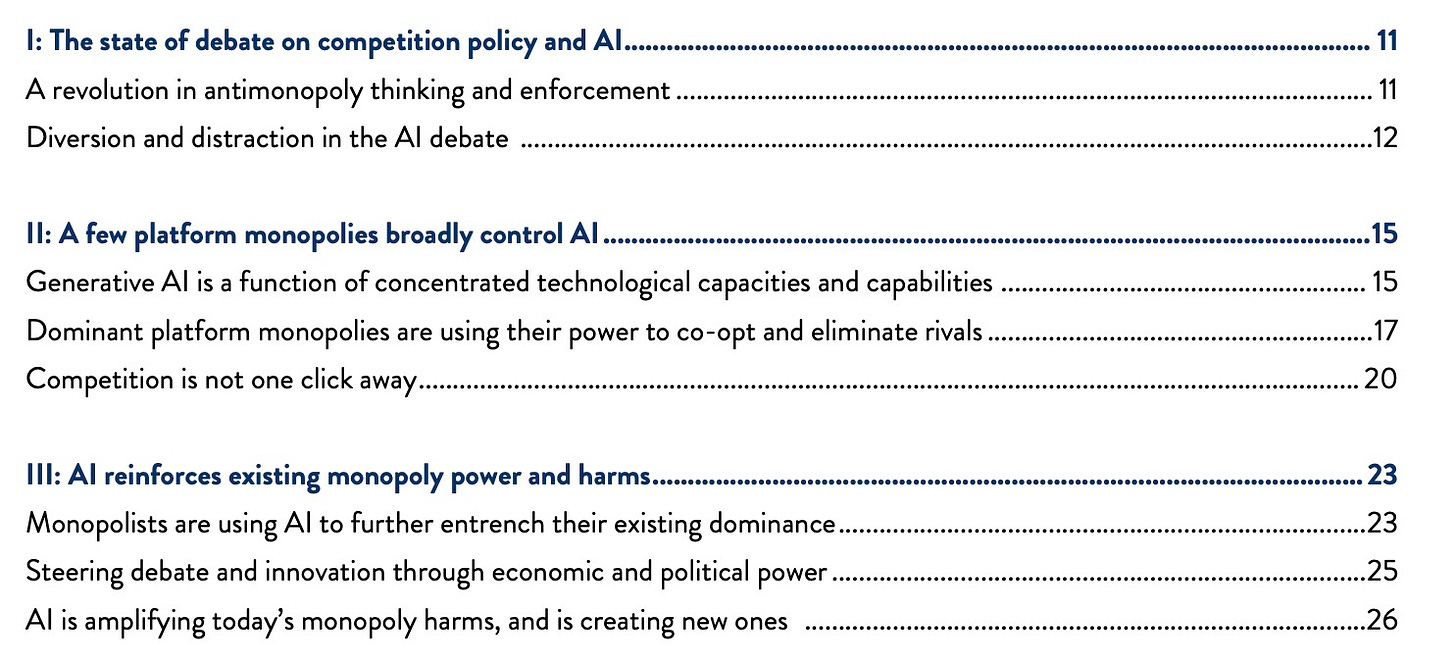
I decided to post the second half of my article this week when I started to read the Open Markets Institute report1, whose table of contents is excerpted above, entitled
AI in the Public Interest: Confronting the Monopoly Threat
I expect to be quoting this report frequently in the coming months. For now, because I am running out of space, I will just provide an excerpt very much in the spirit of my AMS Bulletin article, especially the second half copied below.
prowess in AI – particularly when it comes to large-scale models – is heavily dependent on access to advanced technological capabilities and data, both of which are highly concentrated in the hands of a few gatekeeper corporations…it is precisely because the giants possess so much data and computing power that they have chosen to steer AI innovation in a direction that makes maximum use of those assets. These concentrated resources are in large part the result of extreme levels of concentration in digital markets, fortified by a variety of monopolistic conduct that most governments largely ignored until recently.
The second half of my article follows after the horizontal line.
Industry
The automation of mathematics is largely driven by the tech industry, whose values are not generally aligned with those of mathematicians, but no one is talking about this.
Is the drive to automate mathematics primarily a reaction to a perceived need on the part of the vocation, a contemporary expression of our conatus, or does it represent a sequence of intermediate steps in the implementation of a business plan? The role of industry in shaping scientific research and the institutions in which it takes place is well-documented. In contrast, private philanthropy has long been a factor in support of pure as well as applied mathematics. Michael Barany highlights the role of the Rockefeller Foundation and the Carnegie Corporation in creating some central institutions and adds:
The predominance of military and philanthropic funders…meant that a relatively small collection of socially and institutionally well-connected men had a disproportionate influence on the prerogatives that governed access to resources. This shaped not just the fields that were studied and the institutions that grew and thrived, but also the socioeconomic, racial, and gender composition of [the] mathematics community…2
Direct corporate sponsorship of mathematical research seems to have been less common in the past.3 A 2009 symposium in Paris failed in its primary goal: to generate interest on the part of corporations. The following reactions by executives were typical:4
I don't believe in pure research, nor do I believe ... that direct corporate investment in research is the right way to go.
…mathematics for the sake of mathematics is none of the business of corporations.
So the tech industry's new attention to pure mathematics — as evidenced by the increasingly visible participation of Silicon Valley engineers in conferences on automated mathematics,5 and the creation of the multi-million dollar Hoskinson Center for Formal Mathematics at Carnegie-Mellon University6 — appears to be unprecedented. But it's a safe bet that the industry is no more interested in "pure research" or "mathematics for the sake of mathematics" than were the French executives in 2009.
Nor is the industry likely to be interested in protecting the free exchange of ideas that (for the most part) characterize our discipline. "Colleges and universities," writes Reinhold Martin, "still offer precariously sheltered islands of sanctuary and dissent" — "despite their contradictions,"7 he adds. Silicon Valley is a kind of archipelago but it is also a place where dissent is ruthlessly suppressed. Readers probably know that Google fired engineer Timnit Gebru, former technical co-lead of their Ethical AI Team, when she refused to remove her name from an article about the dangers, of bias in particular, inherent in large language models.
An internal investigation has since uncovered a larger pattern of Google silencing research that casts its technologies in a negative light. Over 2,700 Google employees signed a petition demanding more transparency and denouncing “the unethical and undemocratic incursion of powerful and biased technologies into our daily lives.”8
Given the balance of forces, any convergence between mathematics and industry is likely to be realized on the basis of the latter's values. This logically means subordination of critical thinking to the need to maintain profits and a steady flow of investment. This may already be happening. A mathematician who joined a Silicon Valley project showed me the confidentiality and non-disclosure agreement he was required to sign. The conditions in the NDA, which apparently has no expiration date, prevented him from signaling his agreement with an article I published on my Substack newsletter.
Living deliberately also entails modesty on the part of the authors of this collection of essays. How will we argue that we are entitled to speak for "mathematics" as such? What will be the weight of our influence in comparison with the massive carrots and sticks the industry has at its disposal?
History
Historians of mathematics have been vigorously questioning the narratives around proof that are dominant in the writings of mathematicians; but these narratives, misleading as they often are, are at the basis of much of what is claimed regarding the implications of automation.
It gives me no pleasure to recognize that too many of my colleagues among mathematicians believe history of mathematics can only be written by mathematicians. This is not merely because of the many years of experience required for competence in the use of the specialized vocabulary; it is primarily because, they believe, only mathematicians truly understand our objectives. This incidentally raises an interesting question: will AI ever understand our objectives? In other words, is mathematics subject to what is known in the AI literature as the alignment problem? To take an extreme example (but one similar to those typical of the literature), might an AI world government "solve" the Riemann Hypothesis by killing everyone who cares about the answer?
But do we even agree on our objectives? One perspective has dominated media coverage of both the question of proof verification and that of automation of theorem proving, including the coverage in publications of mathematical societies. This perspective, which corresponds roughly to what call the Central Dogma,9 provides the primary underpinning for the sense of urgency that drives much of the discourse around the nature and role of proof in mathematics; it says roughly that a proof is valid if (and only if) it can be expressed in a formal symbolic language. I call it a dogma because it endows projects of formal proof verification with an epistemological centrality that I don't think is justified.
This perspective, like everything else connected to mathematics, or anything touched by human creativity, has its own history. Here professional mathematicians — who are generally exposed to this history, if at all, in a highly diluted form, adequate for motivation and moralizing but not for intellectual rigor — would benefit from "the use of the resources of history to query the self-evidence of our contemporary habits of thought"10 when seeking to come to grips with the implications of the new technologies for the future of the discipline. Again, it's unreasonable to expect everyone with an opinion about the mechanization of mathematics to be deeply familiar with this history.11 But intellectual modesty should compel anyone who offers an opinion for public consideration to acknowledge that ignorance — of professional standards as well as of isolated facts — is as unappealing in history as in mathematics. Moreover, it hardly requires specialized training to be aware that there was mathematics before formalism and thus that mathematics is likely to continue after this perspective has outlived its usefulness. Formalism as an ideology represents only a blip in the long history of mathematics; its expiration date, in other words, is likely to arrive well before that of human mathematics.
In her introduction to a thick volume entitled The History of Mathematical Proof in Ancient Traditions, Karine Chemla is harsh on the failure of philosophers and mathematicians to reckon with the fetishization of certain standards of proof during the colonial period, "in the process of shaping ‘European civilization’ as superior to the others."
What is important for us to note … is that through such non-mathematical uses of mathematical proof the actors’ perception of proof has been colored by implications that were foreign to mathematics itself. This observation may help to account for the astonishing emotion that often permeates debates on mathematical proof – ordinary ones as well as more academic ones – while other mathematical issues meet with indifference. (Chemla, p. 4)
In particular, the "now standard narrative of the early history of proof" — that asserts, among other things, "that mathematical proof, as it is practised today, is inherited exclusively from … Greek ancestors" — was itself shaped by the ideological preferences of the period.
the narrative belongs to its time and the time may have come that we need to replace it. (Chemla, p. 12)
For those willing to take the time to read it, the book Chemla edited is a remedy to the blinkered view of proof that is pervasive in mainstream philosophy of mathematics. As an example I point to a hypothesis Chemla formulates in her introduction, based on a reading of several analyses of ancient texts: that
some proofs were to be read as a kind of paradigm, the text of a proof was not read only as establishing a proposition, but also as a possible source for working techniques. (p. 31)12
Conceiving mathematics on the model of a video game, or a rugby match, where the only goal is to win, misses this kind of reading, where the apprehension of the text by a necessarily human reader is the reason for its existence.
Democracy
The concealed but deeply embedded hierarchical nature of mathematics makes it more vulnerable to takeover by the explicitly hierarchical forces of industry.
…if the change is accompanied by some hardship, so is every step in the progress of the human race… (“Labor-Saving Machinery,” Daily American, December 11, 1879)
Much of the debate over AI focuses on the threats it may pose to democracy, the concern that decision-making will be taken out of the hands of the concerned public and entrusted to automata whose priorities have been defined by the corporations that designed them. It is no secret that mathematics is not run on purely democratic principles. Decisions that determine the priorities of the discipline — in recruiting students, hiring colleagues, publishing articles, or awarding prizes, among other functions — are made by a self-reproducing elite; the material conditions that guarantee the field's survival are obtained by an opaque process of negotiation with public and private funding sources of which no one, I think, has ever attempted to provide a global synthetic account.
The community of active researchers seems largely content with this state of affairs — the elitism and absence of democratic oversight.13 Determination of winners and losers may not be as clear-cut in mathematics as in chess matches or gladiator contests, which end with one king or gladiator standing and the other horizontal on the board or dead on the sand. Nevertheless, if peer review establishes that someone has proved some theorem then the élite can be confident that their decisions have an objective basis, and they can award the job, or the grant, or the prize to an objective winner — provided the theorem is manifestly an object of desire on the part of the community.14
History teaches us that making deliberate decisions about the future of mathematics presupposes a methodological outlook consistent with that of the Chemla book already quoted:
we do not restrict our corpus a priori by reference to norms and values that would appear to us as characterizing proofs in an essential way.
While some readers may dismiss this outlook as dangerously relativist, can't that also be said of the view, promoted by the tech industry, that the future of the discipline is necessarily in need of "disruption"?15 Isn't it rather the case that adapting our vision of the future of the discipline to our current values is the essence of democratic practice? But democracy is hard to implement in the best of circumstances; it's hard even to conceive in a scattered and fundamentally anarchistic (though deeply hierarchical) community like that of mathematics. Is this why some find it easier to entrust our future to the powerful forces of industry, forces that at least know what they're vibratin' about?
Most of what is written about the topic of this special issue presupposes that incorporating new technologies will allow mathematics to thrive and persevere within an unchanging conatus. Venkatesh's essay argues that the values of the profession will in fact be deeply affected by automation. This could be beneficial if it led to a clarification of these values and a commitment to increasing democratic practice in a way consistent with persistent core values. I have argued elsewhere that allowing industry to set the agenda — for example, by participating alongside representatives of the biggest players in Silicon Valley at conferences like those mentioned in an earlier section — is likely to short-circuit the necessary debate internal to the profession.
My mission, such as it is
Why I'm writing about this topic.
Given how difficult it has always been, in retrospect, to predict mathematics's next move, and given the array of forces propelling the discipline in unexpected directions, why am I writing about mechanization of mathematics at all? It is because my conversations with colleagues have convinced me that in their overwhelming majority they do not see themselves mirrored in the narrative promoted by the ballooning literature about automation of mathematics, and they are largely indifferent, if not hostile, to the prospect of fully formalized proofs. This is not, I believe, because of the ingrown conservatism that is the hallmark of any established conatus, but rather because the narrative that is taking shape radically misses the point of mathematics and substitutes for it a domesticated version drained of meaning. And this, in turn, is because it is so much easier to build on an established narrative, the account of progress familiar since the beginning of the industrial revolution, than to tackle the challenge of giving a name to the drive to participate in the mathematical experience and to explain why it is a particularly gratifying way of being human.
Here's a thought to help with that challenge. Many versions of the narrative around automating mathematicians, including some represented in this special issue, conclude with the prediction that machines either will or will not replace human mathematicians. I find it enlightening to compare the prospect to a concert in which machines have replaced the audience rather than the performers.
The technological mindset banishes the contingent, repudiates the singular, obscures the ineffable, discards whatever cannot be monetized. The understanding at which mathematics aims is all of those things.
Chemla's introduction outlines a research programme — in history of mathematics — that aims to "attend more closely to differences between the various practices of proof, thereby breaking down what is all too often presented collectively as ‘the mathematical practice’. " Another aim reveals itself in the light of the present essay: to identify those practices of proof that enhance the autonomy of mathematicians and resist being monetized. Technology, including AI, may be a tool in the pursuit of these practices, but it can never replace them.
I first learned of this report in Rana Foroohar’s November 17 comment in the Financial Times “Swamp Notes.” The title that day was “Who wins in the battle between nation states and Big Tech?” If nation states are likely to lose, mathematics doesn’t stand a chance.
I haven’t seen another mathematician quoting Foroohar, or the Financial Times. I think it’s required reading for anyone who cares about the answer to the question “Will AI change mathematics?”
Michael J. Barany, Remunerative Combinatorics: Mathematicians and their Sponsors in the Mid-Twentieth Century, chapter in B. Larvor, ed., Mathematical Cultures, Springer (2015), 329-346.
Loren Butler Feffer, "Oswald Veblen and the Capitalization of American Mathematics: Raising Money for Research, 1923-1928," Isis, 89, ( 1998) 474-497, traces some of this history. I thank Michael Barany for this reference.
See M. Harris, Mathematics without Apologies, p. 285.
See for example the February 2023 IPAM Workshop on Machine Assisted Proofs, as well as the MATH-AI Workshops at the annual NeurIPS conferences, whose lists of sponsors speak for themselves.
Crypto billionaire Charles Hoskinson was clear about his objectives in his speech at the opening ceremony of his eponymous center.
Martin, op. cit., p. xi.
Meghan O'Gieblyn, "Babel," n+1 magazine, Issue 40, Summer 2021.
Reuben Hersh called it the Mainstream (as opposed to Mavericks).
Lorraine Daston, Rules, Princeton University Press (2022) p. 22. Daston continues: "One of the uses of history… is to unsettle present certainties and thereby enlarge our sense of the thinkable." Living deliberately inevitably requires that present certainties be unsettled. (A review of Daston’s book in this newsletter is overdue.)
It's only because I wrote to historian Stephanie Dick that I became aware of work by Daston and other historians on 19th century mathematicians who were on opposite sides of a debate on the value of algebraic methods in geometry. Only one side of the debate was at all compatible with the future emphasis on formalism.
One doesn't have to look to Ancient Traditions to observe the variability of standards of proof. The Society for Industrial and Applied Mathematics brochure Careers in the Mathematical Sciences lists more than 50 mathematical careers but only mentions the word "proof" once. Even among branches of academic mathematics one encounters very different styles of proof; drawings, often elaborate, are much more central in published articles in geometric topology than in commutative algebra, for example.
(In response to the inevitable objection that the drawing is merely an aid to intuition, or that the eversion of the 2-sphere has now been formalized, I can only say that, in the actual practice of geometric topology, drawing on the blackboard or on the page is central to the process of proving.)
There is a substantial literature opposing mathematical elitism, mainly concerned with education or with questions of the familiar trinity of diversity, equity, and inclusion. The AMS has been encouraging discussion of these issues — see for example the AMS paraDIGMS initiative. Existing attempts to apply the insights of this literature to questions of research look awkward and half-hearted to me. But they pose serious questions that the ideologues of mechanization of mathematics have overlooked. During the Fields Medal Symposium, for example, Philip Ording asked whether a future mechanized mathematics wouldn't inevitably be even more exclusive, since only those with access to high-powered computation would be able to participate.
As far as I know the account of trans-historical mathematics as a community of desire has not yet been written. It feels unlikely to me that any AI will soon be admitted to such a community.
See "Mathematics and the Undead: How Silicon Valley plans to 'disrupt' mathematics", at https://siliconreckoner.substack.com/p/mathematics-and-the-undead.



"to enable OpenAI to raise the tens or even hundreds of billions of dollars it would need to succeed in its mission of building artificial general intelligence (AGI), the kind of AI that is as smart or smarter than people at most cognitive tasks" - I hope you'll write a piece on what the hell is supposed to be meant by the phrase "smarter than people at most cognitive tasks"... I see parallels with this nonsense claim and your critique of the automated math dream.