Thanks are due yet again to Google DeepMind for having provided me with a topic for a quick and superficial post, leaving me time to reflect on genuinely deep questions, like what Kevin Buzzard meant when he wrote that, thanks to his “Formalizing Fermat” project,
a computer will be able to understand some proofs from late 20th century mathematics…
DeepMind’s AlphaGeometry doesn’t bother with the thorny issues around “understanding”; instead, it
…sidesteps the need for human demonstrations [and understanding of any kind, MH] by synthesizing millions of theorems and proofs across different levels of complexity.1
The synthesis was necessary because
… training data of human proofs translated into machine-verifiable languages are scarce in most mathematical domains. Geometry stands out among other olympiad domains because it has very few proof examples in general-purpose mathematical languages such as Lean owing to translation difficulties unique to geometry. 2
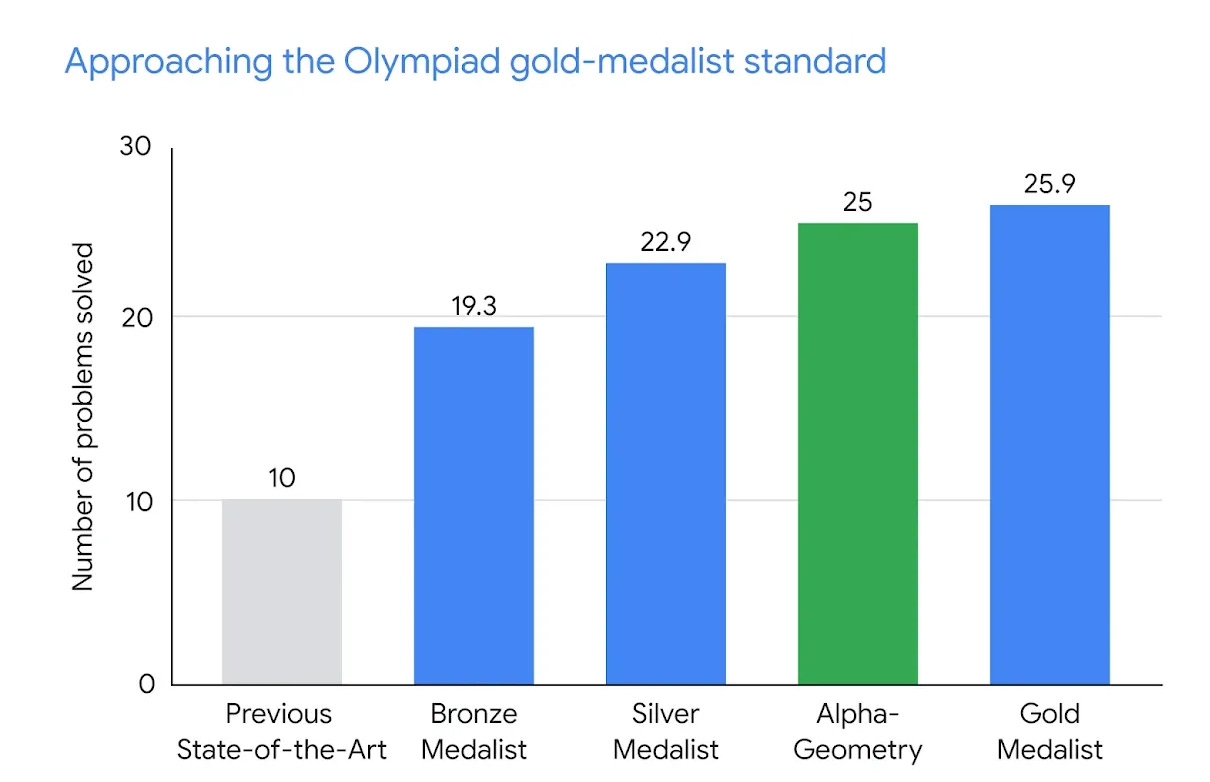
DeepMind’s blog explains how Google’s “generators” found a solution that trained AlphaGeometry to reach the level of gold medalists in the International Mathematical Olympiad (IMO)3:
The lawlessness of large numbers
I first learned about the latest addition to DeepMind’s Alpha line of luxury deep learning products by reading the New York Times article by the indispensable Siobhan Roberts. During the 24 hours between receiving a tip from the (no less indispensable) Margaret Wertheim and actually seeing Roberts’s article, my mind ran through dozens of science fiction scenarios that could be constructed on the basis of 100 million synthetic data points, so that the actual outcome reported by Roberts came as something of a letdown. Of the few lines from the DeepMind blog that Wertheim had shared with me, this one had stood out:
With AlphaGeometry, we demonstrate AI’s growing ability to reason logically, and to discover and verify new knowledge. (emphasis in the original)
Seeing such a bold-faced announcement I naturally assumed that AlphaGeometry could “discover” surprising new insights into geometry. It was only after reading Roberts’s article that I understood that the “new knowledge” was limited to the framework of the Euclidean geometry that has been integral to the curriculum of the West for well over two millenia, and that comprises a substantial portion of each year’s Olympiad problems.
Despite its limited scope, I still assumed that, if AlphaGo Zero could learn to play go at “superhuman levels” after playing a mere 4900000 games against itself, with no input beyond the rules of the game, by generating a billion random diagrams AlphaGeometry would have “learned” all the standard constructions taught in a typical year-long high school geometry course. But it turns out that the system cheats by building heavy-handed hints, like those in the following table, directly into the training data.

If the system needs 100 million examples to train to the level of a top high school geometer, even when the available actions are part of the program, how many examples would it have to run in order to discover without prompting each of the actions in Table 1, 1/3 of which is reproduced above? I’d guess the number would be many orders of magnitude higher. This leads me to suggest the following
WORD PROBLEM: What is the environmental cost (energy, water, carbon dioxide) of creating a training set of 100 million unique examples of IMO-type problems? Express the answer in wash cycles in Mountain View, CA.
A study published last October4 notes that
There is increasing apprehension that the computational resources necessary to develop and maintain AI models and applications could cause a surge in data centers’ contribution to global electricity consumption.
On January 11 I asked Amaury Hayat two questions at the end of his online lecture entitled “The role of Artificial Intelligence in the future of mathematics.” My second question was about the environmental cost of his models that train AI to “have an intuition of Lyapunov functions,” to control differential systems, and — “inspired by the success of AlphaZero” — to search for proofs by treating mathematics as a game. Hayat replied that the carbon footprint could be computed and, as far as he could tell, it was “pretty bad.”
Deep learning should be able to make short work of the above word problem. A serious attempt to estimate the carbon footprint of training GPT-4 concludes that it’s “the same as the annual emissions of 938 Americans.” This is negligeable in comparison to the environmental cost of Bitcoin5, for example, but the study points out that this figure “pale[s] in comparison to the environmental impact from other stages of an AI model’s life cycle, e.g. the deployment stage.” AlphaGeometry, unlike ChatGPT, is not expected to attract 180 million users; on the other hand, no one knows how much this and similar applications of AI to mathematics will eventually cost the environment. Very few people seem to care; and no one expects Google’s dirty laundry to pile up to offset DeepMind’s carbon footprint.
A digression (that is not really a digression) on billionaires
It has become increasingly difficult to ignore the growing influence of decisions by billionaires on the direction of mathematics. It’s not surprising that today’s Billionaires, like the Ultra-High Net Worth Individuals (UHNWI) of past eras, are deeply possessive of the institutions of higher education, to the point of paying to have the institutions named after themselves. Their kind attention to mathematics, apparently a more recent phenomenon, became visible to anyone willing to see it when a consortium of individuals who had made their billions in the tech industry created the Breakthrough Prize “so that scientists are glamorized” in a way an UHNWI can appreciate.
It’s easy to obsess over billionaires, especially when they have the power of life and death over your chosen vocation, and I will have to give this topic the attention it deserves in the future. For now I just want readers to remember that we’re only reading the news about how DeepMind’s latest invention “is coming for your mathematical lunch” because some billionaires are willing to provide the means for generating a billion random diagrams. The first question I asked Hayat6 was whether the training for his proof search project would be possible without the massive resources that only the tech industry has at its disposal. I was not surprised to learn that the training was carried out “with Meta’s Evariste AI team”; an academic department would not have been an option.
Will AlphaGeometry ever matter to geometry?
Michael Barany, a historian of mathematics and science at the University of Edinburgh, [who] said he wondered whether [solving Olympiad problems] was a meaningful mathematical milestone. “What the I.M.O. is testing is very different from what creative mathematics looks like for the vast majority of mathematicians,” he said.
(quoted in S. Roberts’s New York Times article.)
Do the Alpha projects matter? In 2021 a Forbes journalist called DeepMind’s AlphaFold, which predicts the 3-dimensional geometry of protein molecules, “The most important achievement in AI — Ever”7 for its potential to “revolutionize our understanding of biology” and contribute to the discovery of new therapeutic drugs. Go players, for their part, claim the game has changed, now that professionals are all studying the moves of DeepMind’s AlphaGo and AlphaZero.8 But what will AlphaGeometry change? The main purpose of the IMO is to stimulate interest in mathematics and to provide medalists with a credential that will help them compete for the most prized places in higher education. No one is suggesting that AlphaGeometry will soon be taking the place of math majors in undergraduate classrooms. So what is the point?
The style of DeepMind’s announcements of “breakthroughs” is by now familiar, with the obligatory Nature article accompanied by articles in the major international press, the whole orchestrated for maximum impact, with the information strictly quarantined so that the press release, the Nature article, and the press coverage are all made public at the same time. If AlphaGeometry is to be more than another such publicity stunt, it has to look convincingly like a step in the direction of something much bigger, which may or may not be identified with the ultimate goal of Artificial General Intelligence. But, as the above quote from Michael Barany makes clear, no reason has been given to believe that AlphaGeometry is a step in the direction of anything but itself.
Here’s a test. Forget the pre-installed table of standard constructions in Euclidean geometry. Instead, give AlphaGeometry 2.0 the list of axioms and let it generate its own constructions for as long as it takes. Then wait to see whether it rediscovers the Euler characteristic.
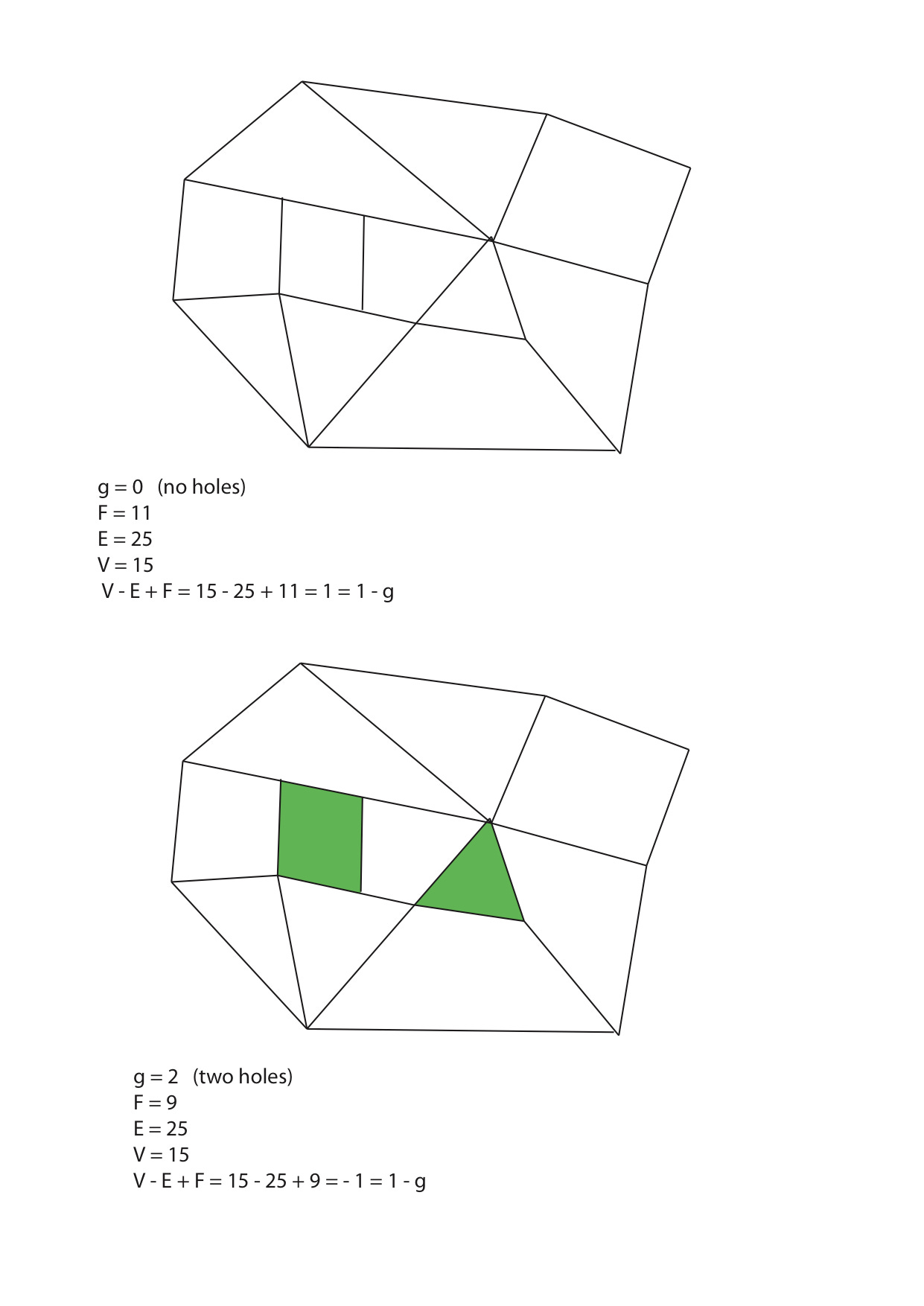
All readers who are not mathematicians need to know is that the Euler characteristic is perhaps the simplest measure of topological complexity. In the figures above, the complexity is identified with the number of holes (the genus g) in the figure. The top figure has no holes, while the two green spots are supposed to represent holes in the bottom figure. Euler discovered a remarkable property of polygonal diagrams in the plane with no holes, like the one on the top. If V denotes the number of vertices, E the number of edges, and F the number of 2-dimensional figures, then V - E + F = 1.
Note that I wrote that Euler discovered this property; I didn’t claim that he proved it. It nevertheless counts as one of Euler’s most important contributions to mathematics.9 Imre Lakatos’s retelling of the story of successive incomplete attempts to prove this property was a landmark in the history and philosophy of mathematics, and should be read by everyone tempted to conflate understanding with reasoning.10
For diagrams of genus g the formula is V - E + F = 1 - g. This11 is the paradigmatic example of a local-global principle in mathematics. There are no holes in the building blocks of the polygonal figures — the points, line segments, and polygons; the holes arise from the way these are put together. Nevertheless, one can identify the most salient features of their configuration — the holes, in this case — by counting the number of building blocks. If you think about this the right way you should find it so eerie that it will make your hair stand on end.
If AlphaGeometry 2.0 rediscovers the Euler characteristic entirely without prompting, even in Euler’s case of genus 0, simply by analyzing the statistical correlations, I will begin to be impressed. I will even be more than mildly impressed if it discovers the “concept” of a hole (in the way that Google “invented the concept of a cat” in 201212). If not, I will consider the project to be a dud.
T. H. Trinh et al., “Solving olympiad geometry without human demonstrations,” https://www.nature.com/articles/s41586-023-06747-5
Ibid.
This annual contest, that has launched dozens (if not hundreds) of high school students on the path to successful careers in mathematics, even has its own hymn
… and a theme song that for some reason features the words
And I know I’m young and strong as the golden sun…
All is fine in love we are one!
A de Vries, “The growing energy footprint of artificial intelligence,” Joule 7, 2191–2194, October 18, 2023.
By implementing Proof of Stake instead of Proof of Work, Ethereum — the source of the fortune behind the Hoskinson Center for Formal Mathematics — claims to have reduced its own carbon footprint by more than 99.99%. But Forbes is skeptical about the figure.
This is a reconstruction from memory. I expected to hear my question on the recording of Hayat’s talk but — I don’t want to be paranoid — it doesn’t seem to be there.
R. Toews, “AlphaFold Is The Most Important Achievement In AI—Ever,” Forbes, October 3, 2021.
https://hajinlee.medium.com/impact-of-go-ai-on-the-professional-go-world-f14cf201c7c2
Ask ChatGPT if you don’t believe me. I did and was not surprised to see the Euler characteristic at number 8 on Euler’s top ten list.
I will return to this important example in the future; in the meantime, you can read this earlier post.
As ChatGPT failed to acknowledge, even after a good bit of nudging.
Including a visual recognition module would naturally be cheating; one would hope a self-driving car would know something about the concept of a hole.



Touche MH. I will be very impressed if the AI discovers the concept of a hole. Then it can go find one and fall into it forever.
Current ML models lack any substantial mechanism for self-reflection or meta-reasoning which makes them particularly poorly suited torward mathematics. I don't think this is an insurmountable problem but it will require some important advances in representing things like beliefs and propositions that current models are unable to perform.
I predict we are going to see a ML models quickly master the kind of tasks that people do effortlessly (speak, walk etc) and this will revolutionize media and art but then we'll hit a plateau while we wait for new conceptual advances in ML that will allow for more systematic reasoning combined with this kind of intuition training.