Kevin's all-synth techno band covers Andrew's greatest hit
Part one of a vision of a possible synthetic future for mathematics and music
Nearly three months after starting this post I am still struggling to tie together the loose ends. I hope Part two will be finished no later than early January.
Flashback to April 1993 (FLT minus two months)
It feels like an epoch ago, the night I was sitting in a car hurtling down the motorway from Cambridge to London, with Kevin Buzzard and two of his friends. But it was only the last century. Kevin had not yet finished writing his thesis with Richard Taylor1, and I was visiting the brand new Isaac Newton Institute for a program called L-functions and arithmetic. Two months later the Newton Institute would chisel its name into mathematical history when Andrew Wiles chose to unveil his proof of Fermat’s Last Theorem in the Institute’s lecture hall. But that night in April I was joining Kevin and friends for an excursion to a techno club. In those days electronic rhythms had become pervasive in central London, where the soundtrack to the simplest purchase of a T-shirt ran a minimum of 120 beats per minute, and Kevin had offered me a chance to experience the music without the distraction of shopping.
My exposure to the music was too brief to leave me with anything more than a hazy sense of the fine distinctions that could be made in the training set the DJ had selected from the database of the massive and expanding corpus of electronic dance music. Nor did I dance that night, but hardly anyone else did either, focused as they seemed to be on an incommunicable inner experience. In the end the strongest impression that outing left was less of the music than of the drive down and especially the drive back at what felt like even more breakneck speed. But I’m sure it was the event that cemented a friendship with Kevin that has now lasted over 30 years, during which each of us has undergone phase transitions too numerous to list.
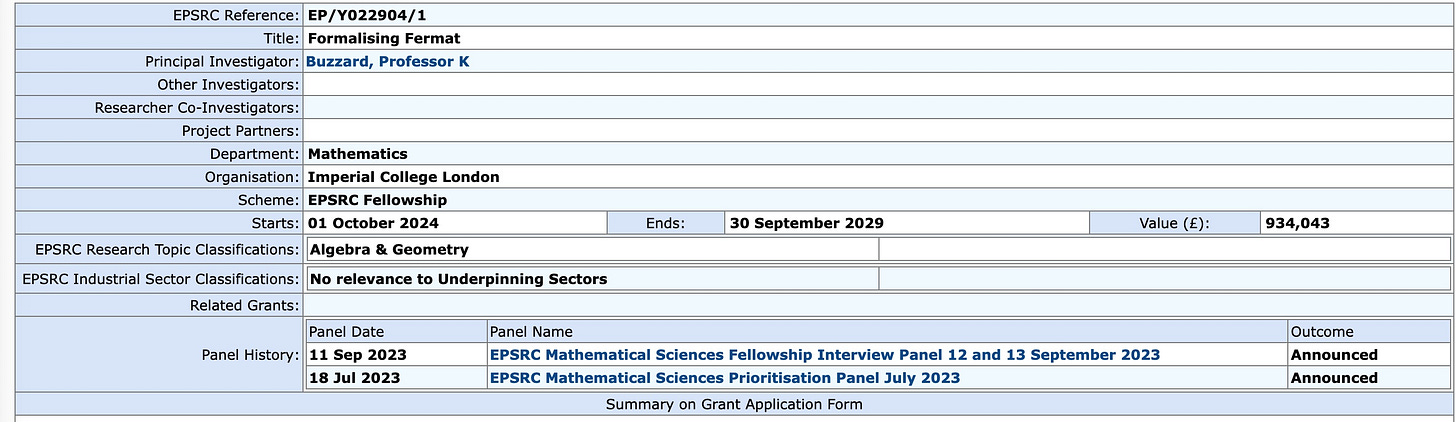
It’s in the spirit of that friendship that I am now subjecting his successful EPSRC grant proposal Formalizing Fermat — which awards £934,043 of the kingdom’s treasure to buy out Kevin’s teaching and administration for five years, so he can devote his full attention to the project in the title — to a close reading.
Computer scientists, and a handful of mathematicians, have been obsessed2 with formalizing Wiles’s proof of Fermat’s Last Theorem at least since 2005, for reasons I don’t really understand. It’s number 33 on Freek Wiedijk’s bucket list of 100 theorems to be formalized3; it’s used to illustrate the Lean language in this recent reference; it probably explains Stuart Russell’s belief that FLT is “perhaps the most famous theorem.”4 In 2019, after a computer scientist friend made several fruitless attempts to convince me to share this obsession, I was inspired to state in Quanta that it is “largely irrelevant to number theorists, and any suggestion that it might be otherwise reflects a deep misunderstanding of the nature of Wiles’ proof and of the goals of number theory as a whole.”
That “largely” was meant to leave room at the margin for Kevin Buzzard and his associates. I still stand by my 2019 assessment, but that margin has undoubtedly been expanding, in large part thanks to Kevin’s efforts as well as the publicity around Scholze’s Liquid Tensor Experiment. It’s worth asking whether the EPSRC is reacting passively to the growing popularity of formalization or whether it hopes to stimulate these developments with the new grant. At the end of Part two I’ll suggest some of His Majesty’s Research Council’s possible motivations.
Kevin’s proposal, verbatim
The text of the grant proposal — more precisely, of the public summary — can be read on the EPSRC website. Since I’ll be quoting it extensively in Part two I reproduce it here:
Mathematics can be viewed as a game with precise rules -- everything is black and white. Computers are nowadays getting very good at such games. Computers can routinely beat the best humans at chess, and with the recent new developments by Deep Mind they can now beat us at the oriental board game Go. Indeed, computer scientists now consider board games to be essentially "solved" -- computers play them better than humans.
But mathematics is different -- it is inherently infinite. For this and other reasons, computers are currently nowhere near "beating" humans at the game of proving new mathematical theorems. However, what is currently within scope is that computers could be used to *help* mathematicians with their research, doing things from checking messy lemmas automatically to suggesting results which may be helpful in a given situation. Perhaps surprisingly, the main obstacle to this sort of progress is that too few mathematicians are engaged with this kind of software, and hence computer proof assistants simply do not know most of the *definitions* of the objects which mathematicians use in their research, let alone the main theorems about these definitions. Computer scientists have already designed tools which can analyse databases of theorems and make suggestions or apply them automatically -- the problem is that the databases do not yet exist.
The proposed research intends to change this. The resolution by Wiles and Taylor-Wiles of Fermat's Last Theorem in 1994 was a highlight of 20th century mathematics, and the tools used (automorphic forms, Galois representations) are still central objects of study in number theory today. My proposal is to fully formalise much of the mathematics involved in a modern proof of FLT in the Lean computer proof assistant, thus reducing the (gigantic) task of fully formalising a proof of Fermat's Last Theorem to the task of fully formalising various results from the 1980s. Such a project will enable Lean to understand many of the basic definitions in modern number theory and arithmetic geometry, meaning that it will be possible to start stating modern mathematical conjectures and theorems in number theory and arithmetic geometry which use such machinery.
Ultimately the outcomes of the project will be that a computer will be able to understand some proofs from late 20th century mathematics, but also many statements of theorems of 21st century mathematics. In particular, this project enables humanity to start thinking about creating formalised databases of modern results in number theory. One could envisage a computer-formalised version of the services such as Math Reviews which summarise modern mathematical research papers for humans, or databases of results in algebraic and arithmetic geometry which can be mined by AI researchers.
A few quick remarks before I return to my holiday break:
Kevin’s observation (or complaint) that “too few mathematicians are engaged” confirms my earlier claim that formalization is “largely irrelevant to number theorists.”
The motivation is markedly different from the concerns Kevin was expressing just a few years ago. In this lecture he cited “nervousness about the state of the mathematical literature” as a reason mathematicians should want to incorporate formal verification into the peer review process. My Quanta article mainly argued that this nervousness was misplaced. Whether or not Kevin is now less nervous, I suspect the proposal downplayed such worries because the EPSRC, a branch of His Majesty’s Department for Science, Innovation and Technology, cares more about Innovation and Technology than about anyone’s metaphysical discomfort.
While computer scientists originally hoped for a formalization of Wiles’s proof, the summary promises to formalize “a proof.” In his very informative October 2 Zulip announcement Kevin is more specific:
“it is a more modern version of the Taylor-Wiles proof which was created during discussions with Taylor on what would be an optimal route to the summit.”
This is completely consistent with the points made in my Quanta article. However, it’s impossible to prove formally that the “more modern version” is equivalent to Wiles’s original proof without formalizing the latter, so I don’t know why the computer scientists who were obsessing about this in 2005 would accept this substitute for the original.
I find the reference to “humanity” here, and also in the Zulip announcement reassuring; Kevin is unafraid to be accused of specism.
Understanding and mining
Kevin squeezes a vast vision of the future into the sentence starting Such a project will enable Lean… but the grammar clouds the vision. Is it Lean that will start stating conjectures and theorems, or is it “humanity”? The sentence is an assertion of cause and (future) effect, with the connection hinging enigmatically on the word “understand.” The different meanings computer scientists and philosophers assign to this word were already explored in this earlier post. When I return to the theme in Part two I will have to account for the new meaning implicit in Kevin’s summary. Although it states explicitly that Lean will be understanding I can’t believe that’s what he really means, because Lean is a programming language and I don’t know what it means for a language to “understand” its textual corpus.
The cause, in any case, is Lean’s future ability to “understand” (or “know”) many definitions, whatever that means. The promised effect (or “outcomes”) will then be a new possibility (for some entity) to “start stating” conjectures and theorems. This looks like a functionalist interpretation of “understanding.” On this view, one doesn’t need to know what’s going on inside the brain, or inside the computer in Kevin’s “outcomes”: it could be a fully furnished scale model of Searle’s Chinese room, for all anyone cares. As long as it starts spouting out conjectures and theorems, we can be satisfied that it has understood the definitions on which they are based.
I’ve already explained why this version of functionalism doesn’t make sense to me, and I’ll have more to say about it in Part two, but I should stress that it is a coherent worldview that is popular among cognitive scientists as well as AI researchers.
Apart from stating new mathematics (“conjectures and theorems”), the promised payoff is a pair of new services: artificial summaries of the mathematical literature (on the model of Mathematical Reviews) and the possibility to “mine” the number theory and arithmetic geometry literature for the precise results one needs. I began to explore what the first service would entail at the end of the last post but ran out of space before drawing my conclusions. It looks like I’ll be giving a talk next February in Paris on what it might mean for a machine — or a human! — to “understand” a proof well enough to summarize its key points, and I will share some of my thoughts before then. As for the second service, just now I asked ChatGPT to “mine” Shakespeare for an example of a verse attributing “understanding” to an inanimate object — on the assumption that Kevin’s attribution of “understanding” to Lean was meant as a poetic metaphor. Instantly ChatGPT suggested this from Macbeth Act 2, scene 1:
Art thou not, fatal vision, sensible To feeling as to sight?
Here Macbeth is addressing his dagger and attributing to it “sensibility” as a surrogate for “understanding.” When I then asked for an example from Shakespeare, or from English poetry, in which the word “understand” appears explicitly, ChatGPT apologized:
I apologize for not having an example with the exact word "understand" in Keats' works or other poets' pieces where inanimate objects are attributed comprehension. This particular word might not be directly used in the context of inanimate objects having understanding in the poetic examples available to me.
Does ChatGPT “understand” the database that it “mined” in order to come up with the Shakespearean quote in the last footnote? The answer was appropriate5 and I suspect a functionalist would probably see this as a clear sign of understanding. What do you think?
Part two will return to the question of “understanding” and will include at least one musical sample.
…with whom I had just finished our first joint paper, along with David Soudry.
Less obsessed, to be sure, than number theorists were during the 3 1/2 centuries between Fermat’s marginal note and Wiles’s solution. I don’t pretend to understand that obsession either, but I have no regrets.
As of two years ago Wiedijk was looking for a PhD student to work on the problem.
But, as Ernie Davis pointed out in a private message, it is also a misreading of Shakespeare, the reference is to Macbeth’s vision of the dagger, which he sees but is unable to feel. David Reed has just posted a comment making the same point.
In the interim, Davis consulted an online concordance to Shakespeare and checked all 100 appearances of the word “understand.” He concludes that
…he does twice use the word "understand" with an inanimate subject, but both of those are puns… Otherwise the subject of "understand" is always a human being [or the devil, in one case], most of the time "you".
It’s striking that ChatGPT is unable (or unwilling?) to use such a familiar index to Shakespeare’s texts.

> However, it’s impossible to prove formally that the “more modern version” is equivalent to Wiles’s original proof without formalizing the latter, so I don’t know why the computer scientists who were obsessing about this in 2005 would accept this substitute for the original.
You have returned to this point many times and I still entirely don't understand why it is relevant.
First note that even if the original version were formalized it would not be possible to prove they were equivalent, for multiple reasons: First, there is not even a well-defined mathematical notion of the equivalence of two formal proofs other than the literal equivalence of two proofs containing the same sequence of steps or, for intuitionistic proofs, the notion of two proofs producing the same function (but Wiles' proof is presumably not intuitionistic and anyways any two functions arising from intuitionistic proofs of Fermat would be the same as they would be functions from the empty set to the empty set). Second, the proofs are of course not equivalent in an informal sense, because the more modern version is, I assume, different in incorporating more modern ideas that allow certain steps of the original proof to be sketched.
But I don't see why computer scientists should care about the difficulties with proving a potential new proof is equivalent to an earlier proof. Was that ever their goal? The original problem of Jan Bergstra specifies "a proof of Fermat's Last Theorem, as proved by A. Wiles in 1995". I think the "as proved" clause is meant to provide proper credit while clarifying if necessary which theorem is meant. "a proof" clearly implies that any proof will do.
The document of Wim H. Hesselink you linked makes clear that the reason Wiles' proof is important to the author is because it also proves the modularity conjecture for semistable curves. It's clear Wim would prefer a simpler proof if it also proves this modularity statement - this is made clear in the third-to-last section. But of course one can verify that a proof proves the modularity conjecture for semistable curves without also verifying that it is equivalent to Wiles' proof.
More broadly I don't see the point in any situation of proving some formal proof is equivalent to some informal proof, and since as you point out the impossibility of this is a tautology, I think it's not reasonable to assume that people who are interested in formalization are trying to achieve this type of proven equivalence. Rather I think people have different motivations. Among these are to be sure that the theorem is correct, which does not require being sure that any past proof is correct.
But even if one's goal is to be more confident that a certain published proof is correct, there is no need to prove that the published proof is equivalent to a formal proof. Simply producing a formal proof and observing that this looks similar to the published proof gives increased confidence that the published proof is correct (in the informal sense used by ordinary mathematicians). Why is this? At least sometimes a serious error exists in a published proof. A few times, such errors have been detected in attempts to formalize a proof (i.e. produce a formal proof similar in some respects to the original proof). On the other hand no serious error can be detected if the proof is not wrong. So it follows that if one produces a formal proof without finding a serious error, the probability that no serious error exists is greater than previously, even if it's possible that a serious error in the original proof was not detected since a somewhat different proof was in fact formalized.
I'm reminded of Sheryl Sandberg's much-ballyhooed concept that if women only "Lean In" to conversations in work meetings, equality in the workplace would automatically result. It seems equally magical thinking to believe that if mathematicians Lean In, understanding will follow.