What is "human-level mathematical reasoning"?
Part 1: which humans ?

Mathematics is unpredictable. That's what makes it exciting. New things happen.
William Thurston, May 14, 2007
It’s a gloomy, rainy, almost wintry day in Paris, which I don’t always love when it drizzles, and I’m starting to write the next entry in this newsletter, trying to figure out what, if anything, Christian Szegedy had in mind when he predicted, as I reported a few weeks ago, that “Autoformalization could enable the development of a human level mathematical reasoning engine in the next decade.” Is there exactly one “human level”? The expression is common among the knights of the artificial intelligence community, whose grail is something called “human level general AI.”
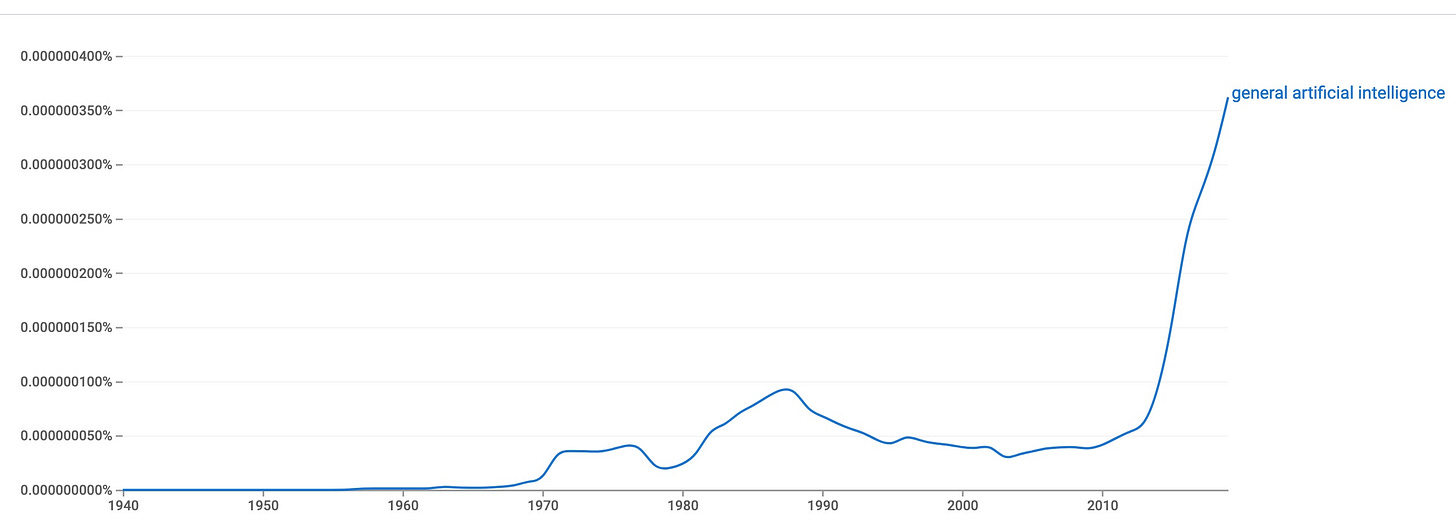
Google n-grams traces the first appearance of the expression “general artificial intelligence” to 1957:
but it is not clear to me whether or not it acquired its present meaning before 1966. The graph reveals a brief growth spurt in the 1980s, before a 20-year long AI winter, at the end of which its frequency took off spectacularly, just after 2010, as the diagram reveals.
The expression “human-level AI” dates back at least to 1984. Here is John McCarthy, who actually invented the term “artificial intelligence” in the 1950s, at a panel discussion in 1984 involving some of the leading experts of the time.1
I have been saying that human-level AI will take between 5 and 500 years. The problem isn't that it will take a long time to enter data into a computer. It is rather that conceptual advances are required before we can implement human-level artificial intelligence - just as conceptual advances were required beyond the situation in 1900 before we could have nuclear energy.
So we can probably date the expression back to the time McCarthy started using it; “human-level general AI,” for which Google cannot plot n-grams, presumably arose spontaneously among practitioners who were already in the habit of using the two preexisting expressions. And talk of “human-level mathematical reasoning” would come naturally to someone like Szegedy, who explicitly promotes autoformalization as a step toward (human-level) general AI.
McCarthy died in 2011, around the time AI emerged from its last winter with the help of big data. By then the AI community had grown more optimistic about McCarthy’s timeline. A report published jointly by the Executive Office of the President, the National Science and Technology Council, and the Committee on Technology2, on the eve of Donald Trump’s election to the presidency, referred to the state of opinion in 2014:
a survey of AI researchers found that 80 percent of respondents believed that human-level General AI will eventually be achieved, and half believed it is at least 50 percent likely to be achieved by the year 2040. Most respondents also believed that General AI will eventually surpass humans in general intelligence.
As far as I know, MIT professor Edward Fredkin didn’t use the expression “human-level reasoning.” He clearly had something more ambitious than the average human mathematician in mind in 1983 when his Foundation established the Leibniz Prize, which, as already mentioned in the previous installment, was to be awarded “for the proof of a 'substantial' theorem in which the computer played a major role.” The prize criterion:
The quality of the results should not only make the paper a natural candidate for publication in one of the better mathematical journals, but a candidate for one of the established American Mathematical Society (AMS) prizes … or even a Fields Medal.
The $100,000 reward may seem like peanuts these days for a human of Fields Medal (or Breakthrough Prize) level, but that’s not how it looked to me when I first heard about it.3 The criterion does offer some perspective on Marcus du Sautoy’s worry whether “the job of mathematician will still be available to humans” when Google is through with us. If “human-level” means “Fields Medal-level” then most humans, it’s safe to say, don’t measure up; and that includes nearly all human mathematicians. IBM’s proof of concept for AI chess performance entailed knocking off the world champion — and I’m still not sure whether it’s purely for technical reasons that Deep Blue doesn’t figure on the list of world chess champions. Szegedy doesn’t specify whether his human level engine has to equal, then defeat Fields Medalists at mathematical reasoning, but what else can he mean? Human travel agents still cater to niche markets; will the Fields Medalists be kept around for similar functions? But who will be the customers?
It has occurred to me, and it has probably occurred to you as well, that the quickest and most cost-effective way for AI to reach human level would be to lower the baseline by “simplifying and degrading” the human control population. The common theme of these biweekly elucubrations is that those of us who are trying to make sense of the promises and threats that AI represents for mathematics are prisoners, myself included, of a discourse echoed by the media but generated primarily for the benefit of a financial ecology with angel investors at the apex. As Marcus du Sautoy wrote in a paragraph I quoted in part a few months ago,
The current drive by humans to create algorithmic creativity is not, for the most part, fueled by desires to extend artistic creation. Rather, the desire is to enlarge company bank balances. There is a huge amount of hype about AI, even as so many initiatives branded as AI offer little more than statistics or data science. Just as, at the turn of the millennium, every company hoping to make it big tacked a “.com” to the end of its name, today the addition of “AI” or “Deep” is the sign of a com- pany’s jumping onto the bandwagon.
The situation is all the more challenging for mathematicians because (to stretch the prison metaphor past the breaking point) the bars that constrain our imagination were forged in large part by a formalist vision of mathematics that fortunately has very little influence on mathematical practice but whose internal coherence and apparent independence of subjective factors gives it a unique advantage in the “marketplace of discourses.”
Until mathematicians come up with an alternative, we are likely to be absorbed by the Silicon Valley business model, as described by Shoshanna Zuboff4:
With this reorientation from knowledge to power, it is no longer enough to automate information flows about us; the goal now is to automate us.
You might think that mathematical humans would resist being automated, but if your ambition is to take home a billion dollars by creating the first mathematics unicorn, you’re likely to take inspiration from Facebook’s redefinition of “friendship,” or to Spotify’s model, which proved, to its ecstatic investors at any rate, that consumers will choose convenience (streaming mp3s) over quality (practically any other medium). Kevin Buzzard actually said that “Spotify has made the world a better place” about 20 minutes into his guest appearance at my course with Spivak last year, citing his own children as witnesses. I don’t really believe that human mathematicians will willingly sacrifice the complexity of our subject for convenience, but then I am probably blind to the potential of mathematics as a revenue stream or as the raw material for any business model.
And keep that word “willingly” in mind as we proceed. I’m as averse as anyone to subliminal manipulation, which is one reason when I put scare quotes around tech slang terms it’s a defensive measure rather than an attempt at fashionable irony. The most insidious manipulation is the one that invades our habits of language. When Pascal wrote, in a passage5 we will quoting more extensively in the future, of
custom, which, without violence, without art, without argument, makes us believe things and inclines all our powers to this belief, so that our soul falls naturally into it…
he could have said: “when you talk like them, you become one of them.” Or alternatively: although we have the impression that we are talking, it’s actually the discourse speaking through us.
But as if to prove that I learned nothing from Pascal, I am tempted to make a suggestion to would-be mathematical unicorn-hunters. Forget about autoformalization. If you really believe mathematics is the road to artificial general intelligence you should take seriously the dignity of the individual mathematical consumer, who is probably a mathematician, and to start by designing a version of Spotify for mathematicians, that will anticipate the articles the individual is most likely to wish to read, based on previous consumption behavior. This suggestion is not to be confused with the lists of suggested articles that publishers already dangle on our screens to the right of the articles we know we want to read. Naturally it would be cheating to rely on metadata — authors’ names, or keywords, or choice of notation — anything that an unintelligent data miner can use to compare a new entry with the existing database. A successful algorithm whose only input is “surplus of meaning” and “unavoidable poetic aspect” is getting perilously close to human level.
Because I find this picture deeply confusing, I’m going to shift the frame slightly. A typical AI success story involves professional musicians unable to distinguish music composed by machines from human compositions.6 In the book I reviewed a few months ago, du Sautoy finds it “very impressive” that 45% of composition students mistook chorales by an algorithm called DeepBach for Bach originals. DeepBach, like most of the algorithms with “deep” in their name, developed its composition skills by a statistical analysis of Bach’s existing corpus of chorales. But if the aim is to “put us [mathematicians] out of business,” this accomplishment would seem to be beside the point, even if anyone thought it made sense to generate new mathematics in the style of Euler, say, by a statistical textual analysis of his collected works.7 I hope everyone will agree that it’s a lot easier to generate new Bach as a remix of actually existing Bach than by either of the alternatives that come to mind: distilling a synthetic Bach using everything that preceded the human Johann Sebastian, or reverse engineering Bach from everything that came after he ceased composing. The latter of these alternatives is intriguing but is hard to imagine in practice, while the former was precisely what central German culture, embodied in the first place in the future Kapellmeister’s notoriously musical human-level extended family, accomplished around the turn of the 18th century.
My thought experiment is an attempt at a response to a challenge that my Paris colleague Jean-Michel Kantor tells me he’s thinking of including in the book he is now writing on AI. When we met in July he expressed his opinion that AI will never be able on its own to come up with the Poincaré conjecture — not even the question, never mind the proof. But since Justin Bieber taught (at least a billion of) us to “Never Say Never,” Kantor is more likely to frame his challenge as a question:
Can a computer come up with the idea of the Poincaré conjecture?
One way to recognize human-level humans is by their propensity to talk to others of their species. You can watch William Thurston speaking about the future of 3-dimensional geometry and topology at Harvard on May 14, 2007, during that year’s Clay Research Conference. I’m pretty sure I was one of the humans in the audience that day, because this week’s epigraph, taken from Thurston’s lecture, was already quoted in the Androids paper that I prepared that same year for the conference that became Circles Disturbed. Thurston was speaking in the wake of Perelman’s proof of his geometrization conjecture, and his title — What is the future for 3-dimensional geometry and topology? — is a recognition that this proof, the one that gave Perelman the opportunity to refuse a Fields Medal and a $1000000 Clay Millenium Prize, separates the past of 3-dimensional topology from its future. “Now we’ve passed that,” he says, three minutes into his talk, “so what happens now?”
Watching this talk again after 14 years convinces me that Thurston’s mathematics and his reflections on mathematics may well be the best challenge to what the AI takes to be “human-level.” He actually says, for example, that “people get interested in mathematics by talking to each other,” that “the important things in mathematics… live in communities of people talking to each other,” — I could just write “He refutes them thus!” in front of a transcription of his talk, “they” being the mechanizers, and let the reader draw the necessary conclusions.
“What’s next?” is the title of a conference held at Cornell in memory of Thurston, two years after his premature death from cancer. I have been unable to confirm that the title is a typical Thurston expression, like “so what happens now?” two paragraphs back. But it could stand in for the question a human-level mechanical mathematician would have had to ask itself at the turn of the 20th century, in order to meet Kantor’s challenge by coming up with the Poincaré conjecture.
The 1982 paper in which Thurston states the geometrization conjecture, which must be one of the most wonderful papers ever written about geometry, is filled with pictures of different aspects of the geometries that arise in the formulation of the conjecture. “The geometric structures turn out to be very beautiful when you learn to see them.”

The paper also provides an extended account of how the author wandered and jumped across the landscape of people talking to each other, and undoubtedly to him as well, about geometry, and eventually arrived at the conjecture.
Thurston’s 1982 paper was a triumph of the human imagination when it was published, and 20 some years later it retrospectively became a triumph of human insight when Perelman proved the geometrization conjecture. Taking up Kantor’s challenge, let’s see how we might mechanize this process, starting with Poincaré — and provisionally ending with him as well, since the story of the original Poincaré conjecture will serve for whatever point we intend to make.
The context for Poincaré’s conjecture about 3-dimensional manifolds was the classification of 2-dimensional manifolds, or surfaces. Closed orientable surfaces are a main theme and source of examples in every introductory course in algebraic topology. The main theorem, due to Möbius, is that such surfaces are classified, up to homeomorphism, by a single invariant, the genus, which is understood as the number of holes in the surface.
This was on Poincaré’s mind in 1892 when he wrote his brief note entitled On Analysis Situs in the Comptes Rendus de l’Académie des Sciences:
…given two surfaces with the same Betti numbers, we ask whether it is possible to pass from one to the other by a continuous deformation. This is true in the space of three dimensions, and we may be inclined to believe that it is again true in any space. The contrary is true.
As Thurston points out at the beginning of his 1982 paper, alluding to a different classification scheme for surfaces,
Three-manifolds are greatly more complicated than surfaces, and I think it is fair to say that until recently there was little reason to expect any analogous theory for manifolds of dimension 3 (or more)—except perhaps for the fact that so many 3-manifolds are beautiful.
Poincaré’s note, which constructs a counterexample to what “we may be inclined to believe” — a pair of 3-dimensional manifolds with the same Betti numbers but different fundamental groups — is reprinted, in an English translation by John Stillwell, in Papers on Topology, Analysis Situs and Its Five Supplements, by Henri Poincaré. (Poincaré used the old term Analysis Situs for what we call topology today.) Stillwell makes a cogent observation in his translator’s introduction.
Poincaré’s topology papers pose an unusual problem for the translator, inasmuch as they contain numerous errors, both large and small, and misleading notation. My policy (which is probably not entirely consistent) has been to make only small changes where they help the modern reader—such as correcting obvious typographical errors—but to leave serious errors untouched except for footnotes pointing them out.
The most serious errors must be retained because they were a key stimulus to the development of Poincaré’s thought in topology.
Now since errors are integral to most approaches to machine learning, which proceeds by successive attempts to optimize some reward or measure of success, we can try to design an artificial Poincaré by studying how error stimulated the original Poincaré’s thought. More modestly, we can design an Artificial Topologist (AT) to track Poincaré’s wanderings and jumpings in the field of Analysis Situs, and see who gets the Poincaré Conjecture first. The AT could just be an algorithm, a silicon-based “brain-in-a-vat” like the carbon-based versions that populate so many philosophical thought-experiments; or it could be a physically embodied companion — like the AF (Artificial Friend) Klara of Ishiguro’s novel Klara and the Sun, who tags along faithfully behind the human teenager she has been chosen to protect — but still an algorithm at its core.
Klara 1.0, the first implementation, is naturally buggy, philosophically even more than technically. Like Ishiguro’s Klara, it is utterly dependent on its human for guidance and direction. While clattering onto the omnibus alongside Poincaré it (she?) will not spontaneously whisper, “Henri, did it occur to you that the transformations you had used to define the Fuchsian functions were identical with those of non-Euclidean geometry?” No, Klara 1.0 is supposed to be reading the texts Poincaré is reading, and those he is writing, and nothing more. When Poincaré asks, “What’s next?” it is understood that the human expects the AT to continue wandering along the humanly predetermined path, only jumping when Poincaré tells it to jump.
Substack is telling me I’ve reached the e-mail limit and it’s time to wrap up. Poincaré accompanied by Klara 2.0, and then Klara 3.0 unaccompanied, will take up the challenge of formulating the Poincaré Conjecture four weeks from now.
Comments welcome at https://mathematicswithoutapologies.wordpress.com/
Annals of the New York Academy of Sciences, Volume 426, Issue 1, First published: 01 November 1984. The other participants in this elite panel were Heinz R. Pagels, Hubert L. Dreyfus, Marvin L. Minsky, Seymour Papert, and John Searle.
https://obamawhitehouse.archives.gov/sites/default/files/whitehouse_files/microsites/ostp/NSTC/preparing_for_the_future_of_ai.pdf
even though I had been introduced to Fredkin by one of his collaborators and I knew, for example, that he owned an island in the Caribbean. Of course I could not have known at the time that more than 20 years later he would sell it to Sir Richard Branson for $20 million.
The Age of Surveillance Capitalism, New York: Public Affairs (2019), p. 15.
“de l’habitude qui, sans violence, sans art, sans argument, nous fait croire les choses et incline toutes nos puissances à cette croyance, en sorte que notre âme y tombe naturellement.”
For example, the article A New AI Can Write Music as Well as a Human Composer on futurism.com. The article, one of hundreds in the same vein, is unsigned and may well have been written by an AI.
Though I confess I would be curious to see the result.