Reverse engineering Poincaré: What's next?
What is "human-level mathematical reasoning"? Part 3
UPDATE, July 17, 2023
A few days ago I received a message from Henry Wilton, a geometric group theorist, which gently pointed out that
A couple of mathematical errors have crept into your analysis which, it seems to me, make some of your inferences invalid.
One of them concerns my reliance on Bartocci’s claim that Poincaré’s homology sphere is “the only possible example” that contradicts the initial form of his conjecture. Wilton explains that this is inaccurate, at least in the sense in which I read Bartocci.
More serious are Wilton’s critique of my attempt to respond to Kantor’s challenge in a way that appears to support Kantor’s skepticism regarding the possibility that Klara 3.0 might spontaneously formulate the Poincaré Conjecture. I will indicate the points below that Wilton argues, convincingly, are dubious. In a future post I will share the relevant excerpts from Wilton’s text and will attempt a different approach to Kantor’s challenge.
I was very pleased to see that Ernie Davis published a seven-page review of the Davies et al. Nature article “Advancing mathematics by guiding human intuition with AI” just a week after the article appeared. The publication of the Nature article upset my schedule and obliged me to split my planned response to Kantor’s Poincaré conjecture challenge into three parts. Davis’s review argues
that the significance and novelty of this application of DL technology to mathematics is significantly overstated in the paper under review and has been wildly overstated in some of the accounts in the popular science press.
In this his opinion coincides with mine, but unlike me Davis is not only professionally competent to make such an argument but is recognized internationally as one of the experts most competent to judge claims about applications of AI. By next spring at the latest I’m hoping to review his book Rebooting AI with Gary Marcus, which has helped to shape my understanding of AI. Davis, whom I know from New York, is sincerely committed to working to help AI realize its promise, so he has to be taken seriously when he writes
The remarkable fame that these works have achieved — the prestigious article in Nature, the excitement in all kinds of science venues across the internet —
has nothing to do with their merits as pure mathematics, and everything to do with the fact that AI was involved. Everyone involved, therefore, has an interest in highlighting and even exaggerating the extent and impact of that involvement.
Anyone who hopes to judge the significance of the developments discussed in the Nature article should read Davis’s review carefully. The AI discussed there, however, is at best at the level of Klara 2.0. That Klara has nothing more to teach us in exploration of the Poincaré conjecture, and it is therefore time to turn to Klara 3.0.
Reverse engineering Poincaré: an exerciseEverything you’ve ever heard or seen or experienced will become searchable. Your whole life will be searchable. (Larry Page, 2001)
Klara 3.0 doesn’t care about your life or my life, or even Larry Page’s life, but is rather searching and collecting, in addition to the whole mathematical corpus, the entire tangible record of the circumstances of Poincaré’s life up to and including 1904. That’s when Poincaré was writing his fifth and last “complément” to Analysis Situs, the one that ends with the question that is remembered as the Poincaré Conjecture, and Klara 3.0 aims to recover that moment by reverse engineering Poincaré.
Stuart Russell argues in Human Compatible1 that
We are a very long way from being able to create machine learning systems that are capable of matching or exceeding the capacity for cumulative learning and discovery exhibited by the scientific community—or by ordinary human beings in their own lifetimes.
Russell specifically points out that
…all scientific discoveries rely on layer upon layer of concepts that stretch back through time and human experience.
and that the “space of hypotheses” that a machine learning algorithm would have to search in order to discover new concepts “becomes simply enormous.” Or, as Peter Scholze put it,
Starting with “human experience,” Poincaré’s reconstructed clone will somehow have to find its way through the “space of hypotheses” to this observation:
There is a manner of representing manifolds of three dimensions situated in a space of four dimensions which considerably facilitates their study.
(Poincaré, Analysis Situs, § 10, Geometric Representation)
Poincaré goes on to describe the representation of his 3-manifold as a polyhedral complex in 4-space. As I write these lines I am reading Bartocci’s excellent article (quoted below), which may not have reverse engineered Poincaré but has come as close as we may wish to reconstructing Poincaré’s thinking as he created the foundations for algebraic topology.
Here is a three-part exercise for a computer scientist who sincerely believes that Klara 3.0 can formulate the Poincaré Conjecture purely by analyzing data, and thus can meet Kantor’s challenge:
Calculate the probability of generating a 3-dimensional simplicial manifold homotopy equivalent to the Poincaré homology sphere at random, and compute the expected running time. (I don’t know how a computer scientist might calculate the probability that Klara has arrived independently at Poincaré’s “manner of representing” 3-manifolds, but we have to start somewhere.)
Same for the probability that a randomly generated simplicial 3-manifold is a triangulation of the 3-sphere.
For a simplicial 3-manifold of given complexity, compute the running time for the calculation of its homotopy and homology groups.
With regard to point 3, it was proved by (my former Brandeis colleague) Edgar H. Brown, in a paper published in Annals of Mathematics in 1957, that the homotopy groups of finite simply-connected simplicial complexes are computable in finite time. He wrote, however, that
Although the procedures developed for solving these problems are finite, they are much too complicated to be considered practical.
The situation may have changed since 1957, but this is not the end of Klara’s troubles, because the word problem for finitely generated groups is undecidable. This seems to mean that it is strictly impossible for any algorithm based on conventional logic to know whether or not a randomly generated simplicial manifold is in fact simply-connected. [NOTE ADDED July 2023: Wilton has given persuasive arguments that this conclusion is not justified. Details to appear in a few months.]
Fortunately, Kuperberg proved that the homeomorphism problem for 3-manifolds is elementary recursive. So it’s not completely inconceivable that Klara can postulate the Poincaré Conjecture as the principal axis of a gigantic correlation matrix before the Sun burns out. But all “elementary recursive” means is that there is an algorithm that runs in time bounded by
steps, which can take a very very long time, probably even for a quantum Klara. And even if the number of exponentials can be reduced, none of the Klaras is allowed to quote Kuperberg’s theorem, because its proof uses (among many other things) Perelman’s Geometrization Theorem, which includes the Poincaré Conjecture, which it would be self-defeating for Klara to quote.
I am actually convinced by the argument from computational complexity that deep learning, no matter how deep, will never match the unfathomable insight of a Poincaré. [NOTE ADDED July 2023: As mentioned above, Wilton has given persuasive arguments that the argument from computational complexity is “beside the point” — and cites work of Thurston himself, with Dunfield, to illustrate why this is the case. Details to appear in a few months.] But this is beside the point, and not only because I believe the computational metaphor of mind should have been outgrown long ago. The point of doing mathematics, as I will continue to repeat, is not to become the world champion at proving theorems or formulating conjectures; the point is that it’s something human beings do. And we (or the human beings among us) do it, as Stefaan Vaes explained to the Queen of Belgium in 2015, “omdat wij dit graag doen.”2 Or to quote Thurston again, from his 2007 lecture:
…the important things in mathematics … are somehow alive; they live in people’s brains, they live in communities of people talking to each other.
The argument from computational complexity has absolutely nothing to do with this. I owe the reader an apology for mentioning them in the same paragraph.
Poincaré's motivations
If mechanization of an established area of mathematics preserves its history it can only be by accident. I have to thank Kantor for giving me an excuse to read Poincaré’s Analysis Situs; I didn’t even know what every topologist must know, namely that the very last sentence on the very last page of the fifth supplement, is not the Poincaré conjecture itself, which Poincaré had stated a dozen or so lines previously3:
Is it possible for the fundamental group of V to reduce to the identity without V being simply connected?
but rather this unconsciously prophetic line:
However, this question would carry us too far away.
By the time algebraic topology reached my generation it had been so thoroughly refined and rationalized that it was impossible for the novice to reconstruct the effort required to develop the original intuition. Poincaré lists his motivations4:
…all of the various paths on which I was successively engaged led me to analysis situs. I had need of the results of this discipline to pursue my research work on curves defined by differential equations [...] and to generalize it to higher order differential equations, in particular to those of the three body problem. I had need of analysis situs for the study of non uniform [i.e., multivalued] functions of 2 variables. I had need of it for the study of periods of multiple integrals and for the application of this study to the expansion of the perturbative function.
Finally, I glimpsed in analysis situs a tool for tackling an important problem in group theory, namely, the search for discrete or finite groups contained in a given continuous group.
The sources of his intuition are so eclectic that it is fair to ask whether there would be anything resembling what we know as algebraic topology today if there had not been one specific human-level mathematician who had extensively explored all these paths.
This morning I woke to a vision of rows of self-driving cars, carrying no passengers, lined up at a drive-in movie theater to watch a short film about self-driving cars. The film reenacts a scene reported in Russell’s Human Compatible, based on a 2018 article5 by D. Sadigh et al., from which the illustration below is taken.

…self-driving cars are notoriously bad at handling four-way stop signs … however, the car comes up with a novel solution: it actually backs up a little bit to show that it’s definitely not planning to go first. The human understands this signal and goes ahead, confident that there will be no collision.… this is a form of communication that the vehicle invented entirely by itself.6
Sadigh et al. stress that this is a creative act on the robot’s part:
None of these plans use any hand coded strategies. They emerge out of optimizing with a learned model of how humans react to robot actions. In the training data for this model, the learner was never exposed to situations where another car … backed up as in (c). However, by capturing human behavior in the form of a reward, the model is able to generalize to these situations, enabling the planner [i.e., the self-driving car] to find creative ways of achieving the desired effects.
Is this the scene where self-driving cars achieve consciousness 7 — the moment, that is, of watching their “purposeful” action reenacted on the big screen, rather than of the action itself? I would pay to watch their headlights glow in self-awareness, even at the cost of being “purposefully probed”; even though just four days ago (as I write this) a Tesla 3.0 taxi went on a 100 km/h rampage, killing one person and injuring 20 more, near the intersection of rue de Tolbiac and avenue de Choisy in Paris, while its (human) driver reportedly looked on helplessly.
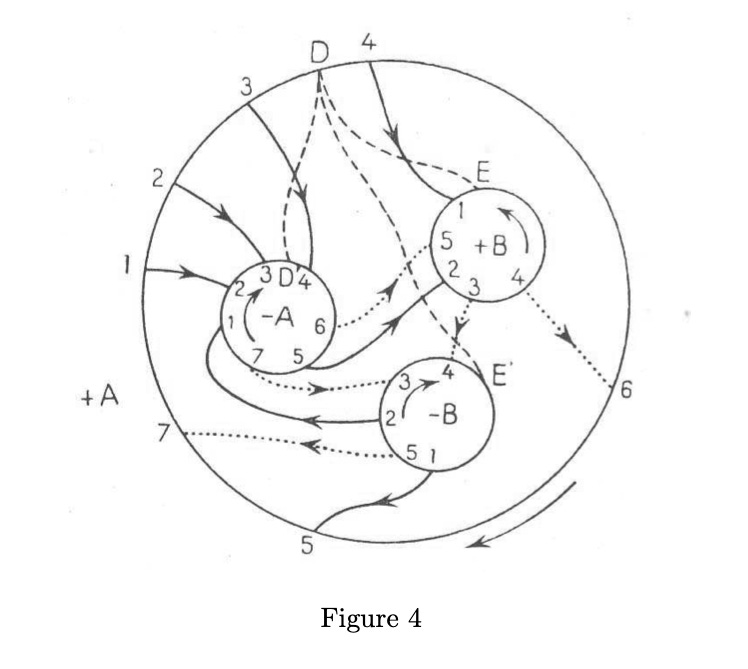
Self-aware or not, Klara 3.0’s job is to recreate Poincaré’s thinking, to let the correct statement “emerge out of” the original incorrect conjecture, after self-training on the counterexample illustrated in the diagram labelled Figure 4. With the help of Bartocci’s article, already mentioned above, I think I can at least reconstruct Poincaré’s argument, though I don’t guarantee that what I’m about to write is correct. Figure 4 is a surface W of genus 2 that appears as a cross section of the 3-manifold V that will provide a counterexample to the original conjecture; more precisely, the markings indicate how V is obtained by gluing two 3-manifolds with boundary along their common boundary W. The solid curve on the left from the point marked 1 on the outer circle +A to the point marked 2 on the inner circle -A is the cycle C2; the solid curve at the bottom from the point marked 5 on the outer circle +A to the point marked 1 on the inner circle -B is the cycle C4. Although this is not immediately obvious from the picture, these define closed curves in V, and therefore elements in its fundamental group. After a series of calculations Poincaré concludes that C2 and C4 generate a subgroup of the fundamental group isomorphic to the icosahedral group, but that V has trivial first homology (and therefore trivial second homology, by the duality theorem that Poincaré also proved, not quite correctly, in the Analysis situs series). Thus Poincaré scrapped the original conjecture and asked the question that, famously, “would carry us too far away.”
“How,” Bartocci asks, “did Poincaré arrive at producing his example?” It’s worth quoting him in detail.
This is, of course, an unanswerable question: we can only hazard some guesses. We can safely assume that Poincaré was not unaware of Felix Klein’s book Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade (Teubner, Leipzig 1884), where the icosahedral group was described in detail. However, there is evidence that Poincaré had no inkling of what today is called the Hurewicz theorem (namely, the fact that the abelianization of the fundamental group is the first homology group with integer coefficients): in fact, he did not exploit the property of the icosahedral group of being a perfect group, and instead explicitly computed both the “homology equivalences” and the “homotopy equivalences” of the cycles 𝐶1, 𝐶2, 𝐶3, 𝐶4. Moreover, it seems certain that he believed that his example was only one among many possible others (“[...] nous nous bornerons à donner un example”), while we know that he stumbled over the only possible example. [NOTE ADDED July 2023: Wilton has explained that this claim is far from accurate, at least on the reading given here. Details to appear in a few months.] In conclusion, we can plausibly suppose that Poincaré essentially proceeded by trial and error, perhaps keeping in his mind (or in the back of his mind) that the icosahedral group could have been a workable algebraic object.
I doubt that anyone at Google cares enough to take up Kantor’s challenge. That’s a shame, because I find it extremely implausible that Klara 3.0 will “stumble over the only possible example” by a random process, or that any Klara not sharing Poincaré’s biography, and the motivations listed in the quotation copied above, would “stumble over” the connection between the icosahedral group and equations of degree 5, on the one hand, and the prefiguration of Morse theory that underlies Poincaré’s synthetic construction of the 3-manifold V.
What’s Next: Turning Mathematics into a Technological Zone
Klara 3.0 has computed herself into a clone of the 1904 model Poincaré. But she aspires to the existential status of Thurston, specifically the Thurston who delivered the 2007 lecture that I attended at Harvard, and the author of On Proof and Progress in Mathematics, which is undoubtedly one of the most influential recent reflections by a prominent mathematician on mathematics as a practice — 945 citations on Google Scholar. Every text I’ve read by Thurston is permeated by a deep awareness of the continual evolution of mathematical values and by a perceptible struggle to maintain his own values in the face of this evolution. It’s no surprise that Thurston’s Proof and Progress is particularly appreciated by those who adhere to a “humanistic” view of mathematics, as represented for example by the Journal of Humanistic Mathematics that began publication in 2011.
Industrial production, in contrast, is accompanied by standardization, and the vision of industrial production of mathematics is presumably no different. The aim of mechanization of mathematical proof is to transform mathematical practice into a technological zone, as defined by Andrew Barry8:
A technological zone can be understood, in broad terms, as a space within which differences between technical practices, procedures or forms have been reduced, or common standards have been established.
It can be argued that standardization is not unique to industrial processes, and that mathematicians would be unable to communicate without sufficient standardization to constitute a common language. The development of standard axiom systems for mathematics at the beginning of the 20th century may have done very little to reassure philosophers concerned with the truth of mathematics, but they unquestionably facilitated mathematical communication. Most mathematicians are uncomfortable with the strictures of the Bourbaki style, but Bourbaki provided and still provides a common language for many central areas of research. Textbooks used in advanced undergraduate courses, often influenced by Bourbaki, do so on a larger scale. And fields can be said to have reached maturity when they have standard references, like Éléments de géométrie algébrique of Grothendieck and Dieudonné in algebraic geometry, now largely supplanted by the Stacks Project; or the Proceedings of the 1977 Corvallis summer school that provided standards for the Langlands program, which a group of younger specialists has decided is ripe for a more systematic update; or for that matter like the algebraic topology textbooks from which mathematics students around the world learn a common vocabulary and style of reasoning, whose roots in Poincaré’s Analysis situs are buried under more than a century of sedimented practice.
Mathematics for the Thurston of 2007 was nevertheless very different from a technological zone. Or perhaps, in view of the standardization of language I just described, I should say he calls explicitly for communication across successive technological zones. And although only a brave professor would dare to use Poincaré’s Figure 4 to teach homology in an introductory algebraic topology course, with a minimum of effort (and with the help of historians like Bartocci) we can still communicate with Poincaré’s shade and read his Figure 4. Just under halfway through his 2007 talk, Thurston proposes the interesting notion of “thought-rot” as an analogy to “bit-rot.” The latter refers to a computer program, like the ones he used to communicate his geometric vision, that no longer works because its operating system has been discontinued. Thurston sees something similar happening to human thinking: “thoughts that used to work stop working” when mathematicians as a community give up one way of thinking in favor of another.
Thurston doesn’t point out, however, that different forces drive the two processes. Several generations of mathematicians had to rework the ideas introduced by Poincaré’s generation before Eilenberg and Steenrod were confident enough to write a book, entitled Foundations of Algebraic Topology, that could serve as a suitable basis for a standard graduate course. The process was naturally driven by a self-appointed elite but it respected the values of the discipline, while redefining them for the next generation. Perhaps each new version of the Macintosh operating system, on the other hand, “makes the world a better place” in the same way that Spotify did, according to Kevin Buzzard; but at the same time it eventually makes my archives, my records, my memories inaccessible to me, for reasons that are primarily commercial.
When the answer to "What’s Next?" is "More of the same"
It’s time to put in a good word for homeostasis. We wouldn’t be worrying about a climate crisis if we weren’t deeply attached to stability. Keeping the earth inhabitable is one of AI’s invariable selling points. Siri, Alexa, and the other entrants in the Klara 1.0 pageant are also primarily designed to provide more of the same. My telephone, and yours too, can write the messages you actually need in the form of decision trees. You type “I’m” and in a series of choices to click one of three nodes the phone will guide your composition of a useful sentence like “I’m going to be late for dinner.” Would you really need to write a poem to convey that information? Did Poincaré really need to formulate his conjecture? How different would the 20th century have been if he had been content with more of the same?
I’ve been thinking again about the idea of reverse engineering Bach on the basis of the history of music after he ceased composing. The idea has obvious conceptual difficulties, but I thought I would conclude this three-part essay by sharing my own experience with Google’s attempts at reverse engineering me, about a year after the first Covid wave in New York City. A few months earlier, my wife and I had spent an hour or two one locked-down rainy afternoon watching YouTube videos of music from the various countries and cultural traditions with which we had direct experience. As the second wave began to crest we finally broke down and purchased an absurdly cheap moderately widescreen TV. After declining to activate its built-in Alexa I decided to test its built-in speakers by watching a few YouTube music videos with which I was already familiar. Each new clip updated the list of suggestions on the right of the YouTube window.
Four songs into the test I realized that the top suggestions, without exception, were selected from the other clips we had watched during that afternoon session. I feared no evil, however; we are not yet walking through the shadows of the uncanny valley. Google had indeed identified us within the parameters of its proprietary technological zone, based on a unique playlist that had been compiled on that rainy afternoon and (presumably) never before or since in Google’s data base. But it could not reverse engineer us. Google’s business model, like every business model, requires stability and predictability. To quote Jaron Lanier:9
I’ve noticed lately that anything you can use to write text with that’s digital is starting to try to predict ahead. So we’re letting the past of language control the future of language in a way that it didn’t before. But at the same time, ultimately, the digital world is us stewing in our own juices. That the algorithms are based on taking the past and limiting the future to the past.
Our tastes, like the mathematics of humans like Poincaré, are “wandering and jumpy,” as Thurston put it. Google knew what had been next on that rainy afternoon, but it had no way of knowing what would be next the next time, nor any time after that.
The next installment, probably entitled The Central Dogma of Formalism, will be published three weeks from now.
Stuart Russell, Human Compatible: Artificial Intelligence and the Problem of Control, Viking Random House (2019), Chapter 3. My review of this book will be ready in the next few months.
In September 2015 Vaes expressed this sentiment at greater length in a toespraak published on his home institution’s website, with specific reference to the Poincaré Conjecture:
Wiskundigen zijn gepassioneerd door vaak erg abstracte vraagstukken, vaak tientallen of zelfs honderden jaren oud, en sommige met ronkende namen als de Laatste Stelling van Fermat, de conjectuur van Poincaré of de Riemann-hypothese. Waarom doen wij dit? Mijn eerste antwoord is: omdat wij dit graag doen! Nog beter verwoordde David Hilbert dit op 8 september 1930 in een speech voor de Duitse vereniging van natuurwetenschappers en artsen. Hij verdedigde met veel passie het belang van onderzoek gedreven door nieuwsgierigheid, en besloot met: “We moeten het weten, we zullen het weten”. Ik kan iedereen aanbevelen om de radio-opname van de dramatische finale van deze speech te beluisteren.
This doesn’t look like the Poincaré conjecture as we understand it but that’s what it meant to Poincaré, who had introduced “simply connected” in the Second Supplement to Analysis Situs as a synonym for “homeomorphic to hyperspheres.”
Translated in Bartocci, “Analogy and invention Some remarks on Poincaré’s Analysis situs papers,” in The Philosophers and Mathematics. Festschrift for Roshdi Rashed, ed. H. Tahiri, Springer (2017).
Dorsa Sadigh et al., “Planning for cars that coordinate with people,” Autonomous Robots 42 (2018): 1405–26.
Russell, op cit., Chapter 10.
Whether or not the cars would be conscious can actually be determined quantitatively using G. Tononi’s Integrated Information Theory, but I haven’t attempted the calculation.
Andrew Barry, “Technological Zones”, European Journal of Social Theory 9(2): 239–253.
https://www.nytimes.com/2021/11/11/opinion/sway-kara-swisher-jaron-lanier.html?showTranscript=1.



