(My) shallow thoughts about deep learning, I

The June workshop on "AI to Assist Mathematical Reasoning," three sessions with (mostly) mathematicians.

The markets for apodictically certain truths or for inputs to the so-called knowledge economy may some day be saturated by products of inexpensive mechanical surrogate mathematicians.

                                                          (MH, Mathematics without Apologies (2015), Chapter 1)

I thought I would be able to squeeze reports on four panels into a single post, but after only three I’m already past 3600 words. Reports are being entered as I watch the sessions, and even at 1.5 normal speed the process is slow and I’m less than halfway through The Workshop. The big surprise so far is that the first session with Stella Biderman of Booz, although it had little to do with mathematics, is (by far) the one that most directly addressed the questions that interest me; but the report on that one is still several weeks away.

The grading system was explained in the previous post. Nine readers cancelled their (free) subscriptions after that post. Substack doesn’t have a complaint box, so I can only speculate on the reasons for their departure. On the other hand, five new ones joined. The total number remains just short of 700.

Day 3, ROLES FOR STAKEHOLDERS IN ADVANCING AI FOR                                                          MATHEMATICAL REASONING

First, a detour through the first session I actually watched.  This was the final panel, entitled Perspectives of Mathematical Organizations,  the one that brings together representatives of mathematicians' professional institutions: 

Gunnar Carlsson, American Mathematical Society (AMS)

Brendan Hassett, Institute for Computational and Experimental Research in Mathematics

Dima Shlyakhtenko, Institute for Pure and Applied Mathematics

Suzanne Weekes, Society for Industrial and Applied Mathematics

I chose to start with this group in keeping with my conviction that, whatever colleagues or outsiders may say, at The Workshop or elsewhere, regarding the desirability of developing "AI to assist mathematical reasoning," nothing will happen at the scale envisioned by The Workshop's conveners without the active involvement of institutions.  The role of the conveners — two divisions of the NSF and the National Academies of Sciences, Engineering, and Medicine (NASEM) — is to convene, but not to issue directives to adapt mathematical practice to the new technological reality.  It's the role of the institutions to set the process of adaptation in motion. 

My mental image of the flowchart gets fuzzy after that.  There was no indication that the panelists were mandated to report on their impressions of The Workshop to their respective institutions, whose members are in any case perfectly capable of forming their own impressions of the recorded sessions.  Judging by the moderator's frequent interventions to help keep the discussion on track, it's not clear that the panelists (other than Hassett, who was himself an active participant) had even been following the earlier working sessions.  The presence of the institutions at The Workshop was mainly symbolic, as far as I could tell; they represented the majority of the affected public — stakeholders (the word on the program) who happen to be mathematicians or their students and associates, but who did not actually attend the proceedings — but whether or not they were thinking about initiating adaptations, or whether they had the power to do so, was never made clear. 

For me power was the big unknown hanging over The Workshop, or at least of the (roughly) 1/3 of the sessions I have watched so far.  I'm going to interrupt the report on the last day’s final session and skip back to The Workshop's very beginning on Day 1, when two speakers representing the NSF — David Manderscheid, Director of the Division of Mathematical Sciences (DMS), and Dilma Da Silva, Director of the Division on Computing and Communication Foundations (DCCF) — a branch of the Directorate on Computer and Information Science and Engineering (CISE) — opened the proceedings with what the program called "Motivation."  While their brief presentations were naturally mainly devoted to introducing their respective divisions to the attendees, they did make a few points that may shed some light on how to fill in the gaps in my mental flowchart.  I learned, for example, that CISE's budget, at just over 1 billion dollars, is roughly four times that of DMS; that close to 3/4 of the DMS budget goes to individual researchers; that NSF has 28 Institutes working on AI, and just announced seven new ones; and that AI is "one of ten emerging industries funded under the CHIPS and Science Act"¹.  Da Silva remarked that her Division already invests a lot in formal methods (mainly for software verification) and that "part of our community would benefit a lot from interacting with people in this workshop" — an observation that made perfect sense, although none of the panels I've watched so far said anything about concrete plans to facilitate interactions.  Finally, Manderscheid mentioned that a new Institute may be created under his Division and "AI and its role in mathematics might be a topic there"; he referred to the Liquid Tensor Experiment and Williamson's work with DeepMind as recent highlights, presumably the sort of interaction his Division would want to encourage.

Projects supported by CISE, from Dilma Da Silva’s slide presentation.

So the relevant Divisions of the NSF are thinking hard about funding AI in mathematics; and the professional associations of mathematicians were invited to participate, because… who else can speak for those most directly concerned?  None of the panelists gave any reason, though, to believe that their institutions would create commissions or working groups, or planned in any way to consult their membership, to recommend ways to integrate AI into the future practice of mathematics. 

After the last panel on Day 3 opened with introductions and with generalities about the value of interdisciplinary work, Heather Macbeth, the moderator, invited the panelists to speak about what mathematicians want from AI.  Of course, she said, they wanted "to prove more theorems faster," but what else beside that?

(Here the image of mathematicians as mice on a treadmill flashed through my mind, and as an unseen operator turned up the speed knob I tried to pinpoint the historical moment when proving "more theorems faster" became our principal common aspiration.  I'm not saying Macbeth is wrong; surely those concerned are eager to get the Riemann Hypothesis or the Hodge Conjecture out of the way as soon as possible, in order to move on to … whatever comes next.  But one might wonder why there is no mathematical version of the "slow food" movement, whose goal would be to savor moments of insight repeatedly, preferably in the company of one's peers, in the way one doesn't tire of listening to certain songs.  Whereas when I reread a proof I've already seen it's always for the sake of future productivity, and never for pleasure alone.  Is it that way for you too?)

The panelists seemed to be speaking for themselves rather than for their associations, and gave no sense of how their presence might affect how mathematicians might get what they want from AI, but of course they made some interesting points.  I'll paraphrase a few of them and hope I'm not misrepresenting their intentions.  In response to the moderator's first question:

Shlyakhtenko wants (automatic?) translation from one set of definitions (worldview) into another, so that the mathematics can "stay readable" to scientists who are not fully trained in mathematics;

Carlsson said "I'm very sympathetic, I like the idea of … automated theorem proving and verification of proofs and so on… but it's important to recognize that mathematical reasoning, which is what we're talking about here, is not exclusively theorems and proofs."  Since he was representing the AMS, of which I am a member, on the panel, I expected him here to say something about meaning or understanding, but instead he referred to experimentation and idealized models: AI needs good mental models, and mathematicians [all of us?] should at least be aware of the problems to be solved.

Here Macbeth interjected that some talks had pointed out that there are "really great mathematical problems" out there in the developing fields.  In response:

Weekes asked whether AI can help extract governing equations from data.  New mathematics is needed to understand important new problems (she specifically mentioned climate science).

Hassett, speaking as director of an Institute, whose role is to create communities of people, pointed out that collaboration styles, exemplified by the Lean community, are more complex than is traditional in the field.  To make progress in machine learning one needs the mathematicians who can formulate conjectures and see patterns, but also people who can get the software to work.  Institutions can help mathematicians find those collaborators. 

Weekes and Shlyakhtenko followed up with the argument I would be hearing repeatedly, that the community should evolve to appreciate collaborations, and that efforts such as proof assistants and formal mathematics should be recognized for career advancement; compare this to the LIGO experiment's 1000-author papers!

When Carlsson and Weekes talked about the need for new publication models, given that the referee process is a "huge bottleneck," Macbeth, pointing to the Thomas Bloom example (discussed here), suggested that 10-20 years from now computerized proofs might "possibly speed up the process."

Then Macbeth asked how other core activities will adapt.  This sparked a disagreement between Carlsson, whose "sense is you get 90% — 80% from the virtual conference of what you would get from the in-person meeting," on the one hand, and on the other hand Shlyakhtenko (who stressed the importance of asking stupid questions in person) and Weekes (who stressed the importance of personal "chemistry").  Here I note that, even those who argued for in-person interaction justified it in productivist terms.

Macbeth's final question:  Does our way of teaching have to change so students (and at what stage in their education) can learn to interact with the new technologies?  No other question referred explicitly to practical changes; Hassett's reply was the only one that hinted at such changes and the challenge they represent:

Mathematical scientists have to reflect on how we can provide enough flexibility in how we teach, so that these new things can seep into the curriculum at an early stage.  It doesn't need to be all AI or all formal things, but people can at least get some exposure in how they can use these as tools to generate understanding.

Weekes took the edge off the implicit injunction to change the curriculum by reminding us that "The US is not producing too many STEM-capable students" and that the arrival of AI will increase employment, economic advancement, and general knowledge.

What we saw in this panel were some thoughts about what perhaps should be done, but not plans to make any of this happen.  Perhaps we'll be seeing this in future rounds.

(This is taking much longer than I expected, so I'm going to postpone my report on Ellenberg's concluding remarks to an indefinite future.)

Because the grades you're about to see are so low, I want to stress again that this is not a criticism of the panelists' presentations.  What the low grades represent is the almost complete failure of the panelists to address the questions that interest me.  It's not their fault, of course; they were just carrying out the assignment the organizers gave them.  I do hope future meetings will treat the question of "AI to assist mathematical reasoning" as part of the wider world and not just a matter of purely technical concern.

Final round scorecard:

• Context 0/10.

• Access 4/10. The points are for Macbeth’s final question, and the replies by Hassett and Weekes, mainly on whether teaching and curriculum have to change. To be honest, this was about changing the way mathematicians are trained, not really about access to resources and monopoly control. One may read this particular exchange as a warning that access to pure mathematical research will be lost as resources are shifted to AI and formal methods, but Weekes predicted no such tradeoff would be needed.

• Externalities 0/10.

• Democracy 2/10. This is the panel where I expected something to be said about ensuring democracy in decisions about adapting mathematics to AI. But none of the panelists said anything about that, and if there were questions from the audience they didn’t make it past the Moderator’s content filter. The 2 points are for the need to recognize efforts of the sort highlighted in The Workshop for career advancement.

• Cluefulness 0/10. I saw no acknowledgment of the debates about AI raging outside the mathematical bubble. Please correct me if I’m wrong.

---

Now I return to the beginning of the first day, with two panels on

STATE OF THE ART OF USING AI TO ASSIST MATHEMATICAL REASONING

Day 1, Overview and Grand Vision (finally)

The first panel, moderated by Brendan Hassett, was an Overview and Grand Vision offered by computer scientist Moshe Vardi and mathematician Geordie Williamson.  Williamson and I are in the same field, broadly construed, and I have been writing to him privately ever since the news of his DeepMind collaboration came out.  Both Vardi and Williamson gave very clear and highly professional presentations.  But for the most part their talks were technical and did not address the questions that concern me, so I will not summarize their presentations, and the grades will be low again. 

The fanel included a few revealing moments.  Vardi quoted as if self-evident the following words of Ernst Schroeder:

Vardi had previously asserted, following a 1979 result of Cook and Reckhow, that "A proof is an argument that can be checked algorithmically"; later he drew the conclusion: 

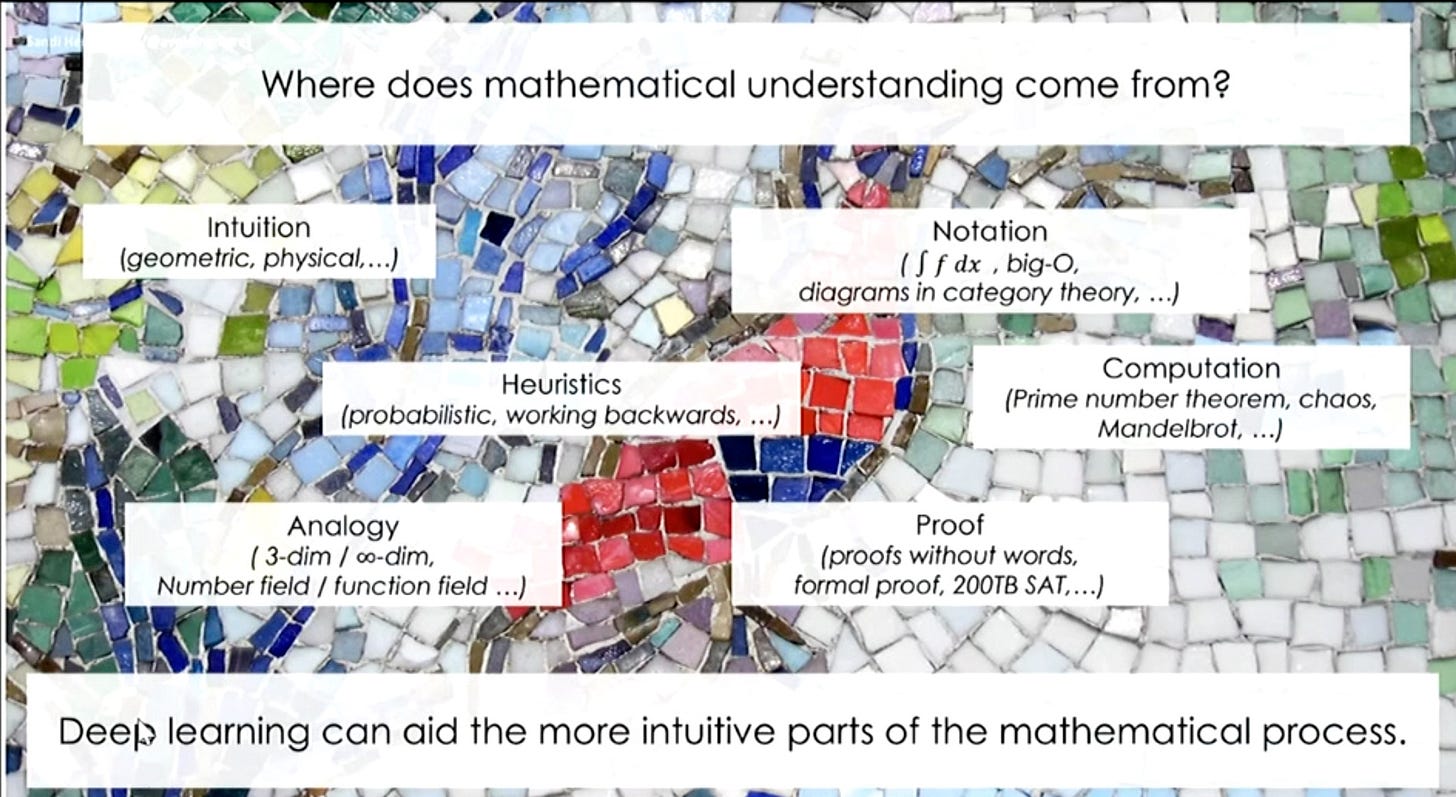
This is certainly one way — a reductive way, in my opinion — to talk about mathematics.  I don't think most mathematicians would agree.  The mathematician Williamson indicated his own priorities — his “vision” of the place of automation — on this slide:

From Geordie Williamson’s presentation, June 12, 2023

Note the modest space Williamson assigns to formal proof.

One of Williamson’s opening slides echoes Jeremy Avigad's emphasis (itself inspired by Thoreau), at last October's Fields Medal Symposium, on the need to "live deliberately."

From Geordie Williamson’s presentation, June 12, 2023

Although he didn't specify what it means to "live deliberately," I am inclined to see it as relevant to all the specific points measured by the scorecard, and most of the points for this panel can be traced back to the implications of this one slide, as well as this point on another slide:

There was a telling moment at the beginning of the Q&A.  Moderator Hassett selected from the chat the question on everyone's minds:

"Will deep learning replace mathematical intuition?" 

Both Vardi and Williamson gave thoughtful and respectable answers, excellent on their own terms.  But neither took the opportunity to question the question; to point out that the question was, in the first place, meaningless; and in the second place, not particularly deep.  

It's meaningless because DL, on its own, can't replace anything.  The meaningful question is whether certain relevant institutions with the power to do so will replace the appeal to mathematical intuition, in their institutional processes, by an application of machines.  I don't know the answer to this question — and The Workshop only gave me the slightest hint of how this will play out — but I know what shape it should take, what kinds of forces will be engaged (see the epigraph above). That's what I mean when I say it's not particularly deep, insofar as history’s depth is driven by social and economic forces.  

The deep problem with the question is the vision expressed by the subtext, which is that the discussion is an example of the historical process of replacing human labor by mechanical labor.  The mistake in this framing can be seen in an analogy that at least some colleagues find apt:  instead of replacing the musicians at a concert, the question is whether DL will replace the audience.²  

Several of the other questions Hassett transmitted — for example, how will ML change our understanding of core mathematical questions; or how does DL change how you choose problems; or how should someone leaving college approach research — were clearly relevant to the future of mathematics imagined at The Workshop. The panelists answered these questions thoughtfully, but each of them could have been the basis for a Workshop of its own; besides, they aren’t directly relevant to my scorecard. One other question from the chat actually does correspond to the item Access on the scorecard:

How do we create an ecosystem³ where someone that isn't directly connected to one of the leading companies in the world or isn't in a top institution can have access to these methods? 

Williamson:  we're very mindful of this and provide resources so that people can learn.  Writing survey papers, education landscape.  Vardi:  (worked at IBM, consulting Intel 20 years)  Cultural gap:  theoretical CS just prove things,  But at Intel they have tools that solve real-life problems and now we have to figure out why.

Day 1, Case Studies: AI to Assist Mathematical Reasoning

The first day’s second panel was moderated by deep learning superstar Yann LeCun of Meta, and again featured one computer scientist: François Charton of Facebook AI Research, and one mathematician:  Adam Wagner, of Worcester Polytechnic Institute. My feelings about Meta/Facebook are even more negative than I've let on, but I found nothing objectionable in either LeCun's moderation or Charton's presentation.  All the audience questions LeCun shared with the panelists were strictly technical. It’s possible that someone watching online had asked why Facebook feels entitled to "disrupt" mathematics, but if so LeCun, who elsewhere has shown an alarming tendency to circle the wagons when his employer’s strategies are questioned, didn't see fit to mention it.  And it's unfortunately true that it would have felt pointless, and been seen as a useless provocation, to raise such a question in such circumstances.  In what circumstances, one may ask, would such a question be appropriate?

I did learn something about the Case Studies from each of the presentations, but nothing that bears sharing here.  One thing I found striking was that Wagner's study involved using reinforcement learning (RL) to find counterexamples to conjectures that can be formulated as games with reward function.  It has frequently been pointed out that mathematics, unlike chess or go, is not a game where success consists in winning something, but Wagner (rather ingeniously) devised reward functions that measure quantities in graph theory whose minimization amounts in certain cases to disproving known conjectures.  Then standard machine learning techniques can be applied to the reward function to guide the search for counterexamples efficiently.  In this connection it may be a pertinent observation that the international video game industry is worth $252.10 billion (according to Yahoo Finance), while the global book publishing (also according to Yahoo Finance) is worth less than half as much.  It may be a bit of a stretch to conclude that the mathematics of the future will look less like narratives than like video games but it's a stretch I'm willing to consider, not least since two contributions to the forthcoming special issue of the AMS Bulletin explicitly compare mechanized mathematics to games.⁴

In response to the question “What are the categories most likely to succeed of mathematical reasoning with AI?” Wagner claimed to be “optimistic that mathematics will be easier than all the self-driving car things” because “in mathematics we only interact with texts, unlike in other general reasoning problems where the other senses are involved.” I should deduct points for “cluefulness” for this observation, which is oblivious to the intensive work, on the part of philosophers and historians, on the role of diagrammatic proofs; it was particularly jarring coming after Wagner’s presentation, which largely consisted in pictures of counterexamples to conjectures about graphs, found with the help of deep learning.

Charton’s answer to the same question stressed the importance of concepts, adding that “Generative models can help with intuition building once you have the right representation, which is again concept-building.” But his answer to the next question suggested to me that he saw concepts as an unfortunate byproduct of human limitations in “high-dimensional reasoning,” and asked: do we want the model of the centaur or the minotaur: is the human doing the thinking and the machine (the animal) the hard work, or vice versa? Will AI proofs be humanly comprehensible?

First round scorecard:

• Context 4/10, for Williamson’s slide “Beware the Hype Machine” and some of Vardi’s comments on working for IBM and with Intel.

• Access 5/10 (very generous in my opinion) for the pertinence of the response to the “ecosystem” question.

• Externalities 1/10, because I optimistically read concerns about energy, water, and respect for intellectual property into Williamson’s injunction to “live deliberately.”

• Democracy 1/10, for the “we” in the “ecosystem” question.

• Cluefulness 3/10, entirely for Williamson’s brief acknowledgment that “mathematicians are typically not used to these discussions,” which hints that others have more experience talking about such matters.

1. This is hardly surprising but was not obvious to me on a casual reading of press coverage of the Act.  Manderscheid just mentioned it in passing, so it's up to the listener to guess what it means.  My interpretation is based on my experience spending summers when I was in high school working in a biochemistry lab and a pharmacology lab.  President Nixon had announced that his own moonshot would be to cure cancer, and the lab directors explained to me that this meant that, in order to continue their ongoing research projects, their grant proposals (the first time I heard that expression) would have to explain their research’s relevance to curing cancer.  They saw this as a minor hassle but not as a serious impediment to doing what they wanted to do anyway, since everything in the field has some natural connection to cancer. 

I don't expect this attitude to work with AI. 

2. See also footnote 4, below.

3. That word again.

4. One of the articles cites Eric Zimmerman’s “Manifesto for a Ludic Century,” which ends with the prediction that

In the Ludic Century, everyone will be a game designer.

and with the reminder that

Games are beautiful. They do not need to be justified.

Both slogans offer an optimistic picture of the future of mathematics in the “Ludic Century” and should be borne in mind by anyone who wants to ward off a future in which deep learning will have “replaced” human intuition.