My benchmark, first two questions
Warning: this post contains mathematics
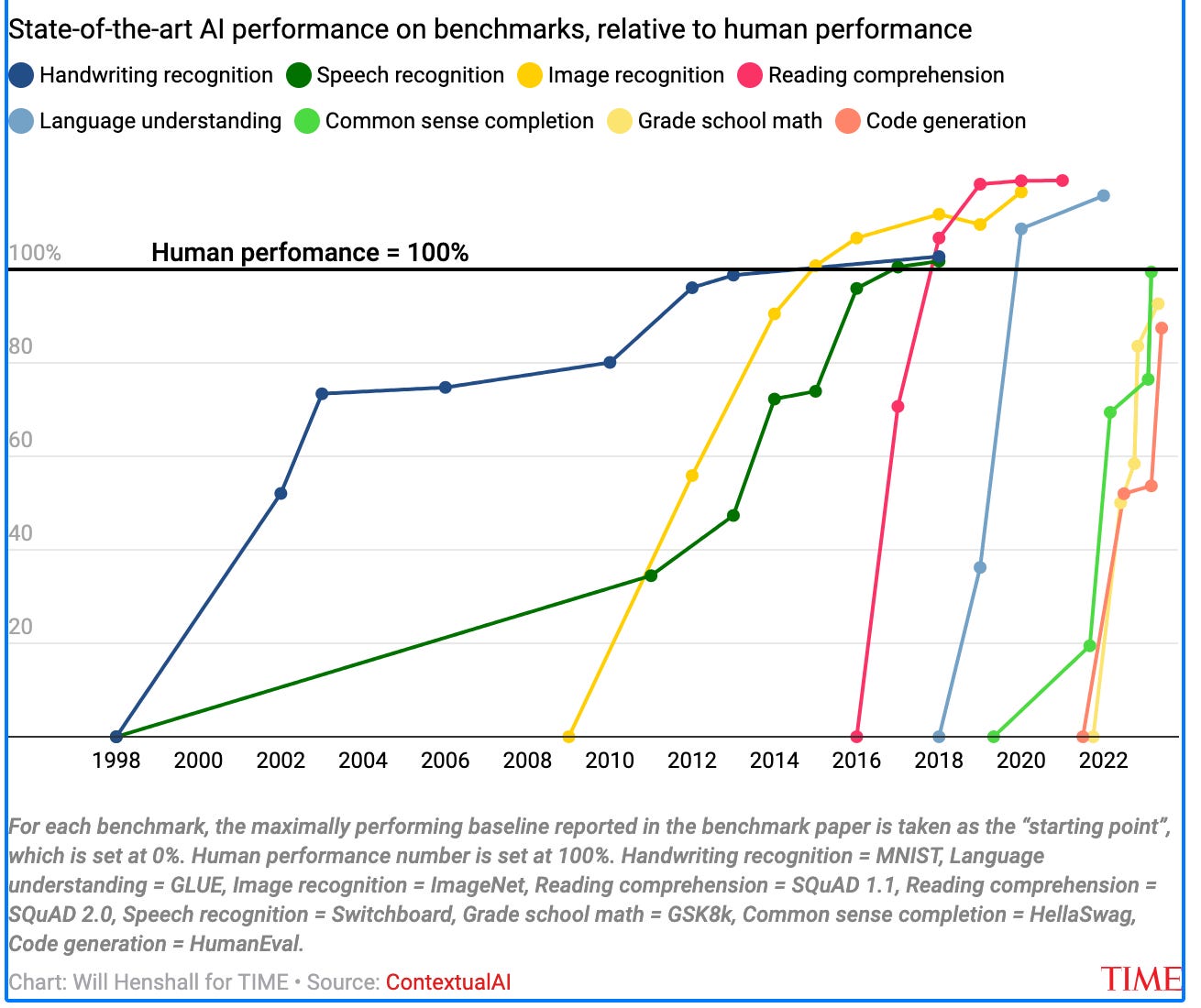
One of the speakers at the January 10 Joint Mathematics Meetings (JMM) AMS Special Session on AI for the Working Mathematician — I don’t remember which one — illustrated his prediction that mathematical AI will soon exceed human performance with a chart similar to the one reproduced above, which measures AI success in various tasks by performance on benchmark tests. A few weeks later a scandal broke around OpenAI’s secret commissioning and exclusive access to the FrontierMath benchmark. As if that weren’t enough to raise questions about ethical standards at Epoch AI — the research institute behind FrontierMath — three Epoch AI researchers, all members of the LessWrong rationalist1 network, have branched out with Mechanize, Inc., a new “startup focused on”
developing virtual work environments, benchmarks, and training data that will enable
nothing less than
the full automation of the economy.
In the meantime, an article by Petrov et al. entitled “Proof or Bluff” looks behind the apparent success on math benchmarks by “state-of-the-art reasoning models” — and discovers “a significant gap in their ability to generate rigorous proofs.” The article’s abstract is unambiguous:

Ernest Davis and Gary Marcus argue that what matters is “the nature of the failure”:
…the AIs were never able to recognize when they had not solved the problem. In every case, rather than give up, they confidently output a proof that had a large gap or an outright error. To quote the report: “The most frequent failure mode among human participants is the inability to find a correct solution. Typically, human participants have a clear sense of whether they solved a problem correctly. In contrast, all evaluated LLMs consistently claimed to have solved the problems.”
But according to a recent article by Princeton computer scientists Arvind Narayanan and Sayash Kapoor — authors of last fall’s AI Snake Oil — this may all be beside the point, for predictions about mechanization of mathematics and of anything else:

Narayanan and Kapoor identify the source of misunderstanding about benchmarks:
The easier a task is to measure via benchmarks, the less likely it is to represent the kind of complex, contextual work that defines professional practice. By focusing heavily on capability benchmarks to inform our understanding of AI progress, the AI community consistently overestimates the real-world impact of the technology.
Judging by the absence of any challenges to the predictions at the JMM Special Session, the professionals most directly targeted by such predictions — mathematicians reading this post, for example — are as likely as the general public to misunderstand what benchmarks really measure.
Ever since the JMM I have been threatening to publish my own Benchmark Problems, and today I will begin to make good on my threat. I’m pleased to point out that my problems, in contrast to those analyzed by Narayanan and Kapoor, have been chosen to “measure real-world utility,” at least for those who believe that mathematicians have utility and that the world we inhabit is part of the real world. Moreover, the problems are freely available to anyone — human, mechanical, fictional, or divine — who wants to try their luck solving them.
There will be no scandal of secret insider access to the solutions, because I don’t know the solutions — nor, as far as I know, does anyone else. What would be the point of proposing a problem I knew how to solve? Besides, less than a year ago I reported that Christian Szegedy was still predicting that we would have to wait until 2029 for a super-human mathematician; but I had not realized that already in February 2024 he had advanced his prediction to June 2026. Elsewhere he had defined a super-human mathematician as one that could prove
10% of problems from a preselected 100 open human conjectures … completely autonomously.
So we human mathematicians had better get on the ball if we’re going to “preselect” 100 open conjectures in time for Szegedy’s mechanical mathematician to flex its super-human muscles. I’m committing to doing my part by “preselecting” and even stating ten of them, two of which are in this post — and I’m demonstrably human. Szegedy will have his full preselection as soon as I complete my quota of 10 and nine more mathematicians step up to the challenge. How about you?
The first Benchmark Problem
Almost immediately after the war Johnny2 and I also began to discuss the possibilities of using computers heuristically to try to obtain insights into questions of pure mathematics. By producing examples and by observing the properties of special mathematical objects one could hope to obtain clues as to the behavior of general statements which have been tested on examples. I remember proposing in 1946 a calculation of a very great number of primitive roots of integers so that by observing the distributions one obtained enough statistical material on their appearance and on the combinatorial behavior to perhaps get some ideas of how to state and prove some possible general regularities. I do not think that this particular program has been advanced much until now. …In the following years in a number of published papers, I have suggested and in some cases solved a variety of problems in pure mathematics by such experimenting or even merely "observing." … By now, a whole literature exists in this field.
(Stanislaw Ulam, Adventures of a Mathematician, Chapter 10)
The aim of this benchmark is to answer a question familiar to people working on the local Langlands correspondence, and specifically a version of the question formulated in my 2002 talk at the International Congress of Mathematicians in Beijing:
This requires some explanation! I’m going to assume for this first benchmark that n is a prime number. The group J is the multiplicative group of a division algebra D of dimension3
Since J is compact modulo its center, every irreducible continuous representation of J on a complex vector space is finite-dimensional; and since n is prime, every such representation of dimension greater than 1 corresponds, under the Jacquet-Langlands correspondence (denoted JL in the excerpt), to a supercuspidal representation π of GL(n,F), and therefore to an irreducible representation σ(π) of the Weil group W(F) under the local Langlands correspondence. Assume then that JL(π) is not of dimension 1. Problem 7 asks for an explicit numerical relation between the character of the finite-dimensional representation JL(π), expressed in terms of the coefficients
and the character of the n-dimensional representation σ(π).
In 2025 I am asking for a bit more: I want a closed-form4 expression for these coefficients in terms of the character of σ(π), or alternatively a closed-form expression for the character of σ(π) in terms of the coefficients. It’s mentioned in the clipping that Tunnell and Saito obtained a numerical relation when n = 2, in terms of the local constants of functional equations. This is a valuable relation — it played an essential role in one of my papers5 — but it is not as explicit as what I have in mind. The local constants can in turn be expressed in terms of Gauss sums, and has a simple form for odd primes p, as indicated in the last sentence of the excerpt; Bushnell and Henniart completely solved the problem after my talk was published. But when p = 2 the expression in terms of Gauss sums is obtained by an elaborate inductive argument, and although it can be computed effectively I don’t see how to turn it into a closed-form expression. For larger n the same difficulty arises for p ≤ n, because it is then not the case that every σ(π) is obtained as the induced representation from a character of an extension of degree n. This is the range I have in mind; the Bushnell-Henniart argument is valid as long as p > n.6
I actually wouldn’t be surprised if Problem 7 were amenable to machine learning! Since the two sides of the correspondence are represented by explicit functions on (conjugacy classes of) elements of finite groups, any patterns underlying the correspondence could in principle be detected by the kind of regression process described in the 2021 Nature article on the collaboration of knot theorists and representation theorists with DeepMind. And if the relation is random, or partially random and partially determined, machine learning could detect that as well. This would look less surprising, and less likely to generate headlines in Quanta, if the procedure were called “statistical pattern recognition” rather than “machine learning” or “artificial intelligence.” The same applies to Problem 7, but I am so strongly motivated by the prospect of giving Szegedy and his boss a head start toward fulfilling his prophecy that I am happy to call this an AI Benchmark Problem.
I already wrote that this problem and the next one are available, free of charge, to anyone with the computing power and the determination to solve them. I am slightly curious to know whether or not the computational complexity of generating enough data to draw meaningful conclusions on Problem 7 can be managed without converting the entire solar system to computronium.7 To be honest, I would be interested to work on this problem myself; but only if it could be done with the resources already available within a university mathematics department, and without any association, direct or indirect, with a corporate AI laboratory.
A second Benchmark Problem

Language disguises the thought; so that from the external form of the clothes one cannot infer the form of the thought they clothe, because the external form of the clothes is constructed with quite another object than to let the form of the body be recognized.
The silent adjustments to understand colloquial language are enormously complicated.
(Wittgenstein, Tractatus Logico-Philosophicus, 4.002)
That last proviso is certainly superfluous; there’s little risk that any of the Magnificent 7 corporations, some of whose human incarnations are pictured above, will be interested in any of my Benchmark Problems. Narayanan and Kapoor’s observation about benchmarks and “real-world utility” can be read in the opposite direction: the fact that corporations like OpenAI are spending money and resources to compete to solve problems of no intrinsic interest means that benefiting mathematical research is not among their priorities. This should hardly be surprising; their priorities come down to profits and market share. I don’t know why so many of my distinguished colleagues are apparently confused about this.
This is why I find it encouraging to read, in a recent paper by nine mathematicians that applies reinforcement learning to a conjecture in group theory, that
this entire project was carried out using relatively modest computational resources that a small academic research group can easily afford.
With this in mind, here is a second Benchmark Problem, in the same area as Problem 7 above. Recall that I assumed above that n is a prime number. For n composite, it is no longer the case that every π such that JL(π) is of dimension greater than 1 is necessarily supercuspidal. Thus we have our second Benchmark Problem:
Problem: Assume n is a composite number. Find a simple8 characterization of those irreducible representations R of the group J of Problem 7 that are equivalent to representations of the form JL(π) with π a supercuspidal representation of GL(n,F).
The last time I thought about this question, there was no such simple characterization in the difficult case when p ≤ n. As far as I know, this is still the case.
And singularitarian, or at least singularity-adjacent.
Ulam is referring to John Von Neumann. I include this quotation to remind readers that post-human mathematics already had a long history when the area around San José was still mainly celebrated for its cherry orchards.
Sorry about the box, it appears Substack’s Latex function doesn’t allow typesetting in the middle of a line.
The expression “closed-form” is left deliberately vague, because it conceals an ontological commitment. We may return in the future to the question of whether machines and humans share ontological commitments, and indeed whether it would be desirable if this were the case.
L-functions of 2 x 2 unitary groups and factorization of periods of Hilbert modular forms. J. Amer. Math. Soc. 6 (1993), no. 3, 637–719.
(With apologies to experts for the imprecision in what follows.) For any reductive group G over a non-archimedean local field of residue characteristic p, Tasho Kaletha has identified a class of regular supercuspidal representations, obtained by the construction of Jiu-Kang Yu and Jessica Fintzen, and conjectured an explicit formula for the Galois parameter associated to such representations, by the constructions of Genestier-Lafforgue and Fargues-Scholze, that generalizes the formula proved by Bushnell and Henniart. Fintzen has shown that, when p is a prime number that does not divide the order of the Weyl group of G, every supercuspidal representation is obtained by Yu’s construction. Assuming Kaletha’s conjecture, the natural generalization of Problem 7 to such groups G is thus only difficult for p small relative to G.
As Kaletha pointed out to me, one could reformulate Problem 7 when G = GL(n) directly for π, without referring to the Jacquet-Langlands correspondence. For other groups G this is the only option. I prefer to keep the original version of Problem 7, because the data are finite-dimensional on the two sides. This may or may not make the computations more tractable but I find it more appealing to remain in a finite-dimensional setting.
This sentence could itself be the basis of yet another Benchmark Problem, but I don’t feel competent to turn it into a precise question.
See Footnote 3.


I'm getting emails from AI startups which want to pay (peanuts) for maths problems to train their models on :-)