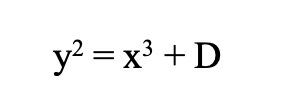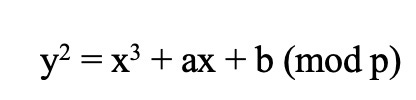Mathematicians challenged by machines
Les mathématiciens face au défi des machines, from Pour la Science, May 2022
This is the first half of the first version of the article I translated into French and submitted for publication in Pour la Science, the French version of Scientific American1. My French text was corrected and reorganized by the editor Sean Bailly, in close consultation with me. I very much enjoyed working with him; he and the editor-in-chief respected my wishes even when they disagreed with them, a welcome change from my previous experiences with commercial publications. Captions and summaries were mostly supplied by the editors, however.
What follows is an amateur history2 of the role of machines, especially digital computers, in the development of mathematics, up to the recent period of automated proof verification, automated theorem proving, and formalization. Some readers may be surprised by its positive attitude. The second half of the French article roughly corresponds to the contents of the text I tried and failed to publish in English and finally made public on this site, but is (somewhat) less polemical.
Substack warns me that this installment is too long for email. Readers will therefore have to read it online at siliconreckoner.substack.com. Comments and questions are welcome at the Mathematics without Apologies blog.
Machines have long had a place in mathematics. The extensive use of mechanical aids to arithmetic and astronomical calculation is already attested in antiquity. The first modern calculating machines were invented in the seventeenth century, when mathematics began to take shape as a separate discipline; Pascal and Leibniz are considered pioneers in mechanical computation as well as in the development of modern mathematics. So it's hardly surprising that digital computers were adopted by mathematicians soon after their first appearance. The possibility of rapid machine calculation played a central role in directing theoretical research, especially in my own field of number theory; I give some examples below. But mathematicians became more ambivalent about computers when they began to participate in proving theorems, an activity previously seen as a unique privilege of human reason.
Historians may see this year as a turning point in the relation between computing and mathematics. In June 2021, a team of mathematicians working with the Lean theorem prover met the challenge, posed in a blog post by the German mathematician Peter Scholze just six months earlier, to formalize a particularly knotty proof he had just completed with his post-doctoral fellow Dustin Clausen. The proof by Clausen and Scholze was written in the usual idiom of mathematical research, where words and mathematical symbols are formed into sentences that follow the grammatical rules of natural language — in English, as is usually the case these days. A formal proof, in contrast, is written in a purely symbolic language. Human mathematicians usually find formal proofs difficult or impossible to understand, like raw programming code. This dependency graph gives a sense of the complexity of the solution to the challenge posed in Scholze's liquid tensor experiment. However, as the Lean Community website explains, "In a formalization, all definitions are precisely specified and all proofs are virtually guaranteed to be correct."
It was this virtual guarantee of correctness that Scholze sought in his post on Kevin Buzzard's xena blog and that the mathematicians working loosely with Buzzard's xena project have now provided. This was considered important enough to merit a long article in Nature.
The international media became aware of Scholze in 2018 at age 30, nine years after his first mathematical breakthrough, when he received the coveted Fields Medal for his work that blurred the border between number theory and geometry. The readiness of a pioneer as influential as Scholze to admit the need for machine certification as a supplement to his intuition will undoubtedly give a boost to the formalization program. Some mathematicians, and quite a few computer scientists, welcome this development and see it as long overdue.
But there is also a vision in which computer-based formalization is a first step toward a model of mathematics in which machines join humans first as colleagues, then as rivals. And the examples of the chess-playing program Deep Blue, and the more recent self-taught go-playing program Alpha Go, are cited as proof that this is a competition humans are bound to lose. Are these hopes and fears realistic?
These days, when every operation in our daily lives is mediated by at least one, and usually several computers, it's easy to forget that the theory of digital computation was invented by mathematicians, during a period of great distress over the foundations of our subject. Early in the 20th century, after the confidence of mathematicians had been shaken by a series of apparent paradoxes, David Hilbert formulated a program, called formalism, aimed at making mathematics capable of verifying the correctness of its own reasoning. Hilbert observed that mathematical statements could be rewritten as strings of symbols, and that a proof amounted to a sequence of transformations of such statements according to the accepted rules of logic, as in the system of Russell and Whitehead's Principia Mathematica. Just as solutions to certain kinds of polynomial equations or differential equations could be calculated from the form of the equation, Hilbert suggested, the existence of a proof of a theorem might be deduced from the theorem's form in a suitable symbolic language. Mathematical reasoning, on this view, was a kind of computation.
Gödel's undecidability theorems famously derailed Hilbert's program, but they also set in motion a decade of intense reflection on the nature of mathematical computation and deduction that included the foundations of the theory, and soon the practical realization, of digital computers. Key figures in this story include Alan Turing, Alonzo Church, and John von Neumann. The ability of the first digital computers to carry out rapid and accurate calculations was soon put to work on a raft of practical problems, most notoriously in the design and deployment of the hydrogen bomb. But the origin of digital computing in the concerns of pure mathematics was never forgotten. A widely-quoted article by Alan Newell and Herbert Simon, published in 1958 in the journal Operations Research, predicted that within ten years, digital computers would reach four milestones, on the way to a "world in which [human] intellectual power and speed are outstripped by the intelligence of machines." One of these milestones was to " discover and prove an important new mathematical theorem." In this way mathematics became one of the earliest targets of what soon came to be known as artificial intelligence.
Pure mathematicians, meanwhile, quickly exploited digital computers as extremely rapid calculating devices. As H.P.F. Swinnerton-Dyer wrote in the mid 1960s,
With the advent of electronic computers, calculations which would previously have been out of the question are now quite practicable, provided that they are sufficiently repetitive. There must be many topics in number theory in which intelligently directed calculation would yield valuable results.
Swinnerton-Dyer had in mind results like the prime number theorem, an accurate approximation to the proportion of prime numbers less than a given integer N. The theorem, which asserts that the proporition is roughly x/ln(x), where ln is the natural logarithm, was proved at the end of the 19th century by the methods of analytic number theory, the application of techniques of mathematical analysis to infinite series. But no one would have thought to prove the statement had it not been anticipated a century earlier by Legendre, and more accurately by Gauss, on the basis of their numerical calculations.
Gauss, the founder of much of modern theoretical mathematics, was also proud of his extraordinary skill at calculation. But Gauss would have been no match for even the relatively primitive digital computers available when Swinnerton-Dyer was writing.
Together with Bryan Birch, Swinnerton-Dyer proposed what is still one of the most important conjectures in number theory, on the basis of extensive calculations using the computers available at that time. The Birch-Swinnerton-Dyer Conjecture (BSD) concerns the existence of rational solutions to elliptic curves — cubic equations in two variables, like
where D is a rational number. Such equations are the simplest for which elementary methods could not — and in general still cannot — determine whether or not the number of rational solutions is finite or infinite3. The question is of an algebraic nature; BSD gives a conjectural answer, along with much more information about the solutions, in terms of the techniques of analytic number theory that were developed in the 20th century.
Swinnerton-Dyer's article contains excellent theoretical reasons for believing in BSD, which since 2000 has been one of the Clay Millenium Problems, whose solution comes with a $1000000 prize. The article also explains how these heuristics guided its formulation and subsequent refinements. But the conjecture would not have won such rapid acceptance if it were not accompanied by the extensive supporting data that only digital computers could provide. Number theorists thus have computers to thank for one of the most fertile areas of research of the past 60 years, including results like the theorem of Bhargava and Shankar confirming BSD for a positive proportion of elliptic curves with rational coefficients, as well as the long list of more general conjectures (Deligne, Bloch-Beilinson, Bloch-Kato, and others) that build on the success of BSD.
A similar story can be told about the Sato-Tate conjecture, which also dates to the early 1960s. If p is a prime number, we can consider the elliptic curve congruence
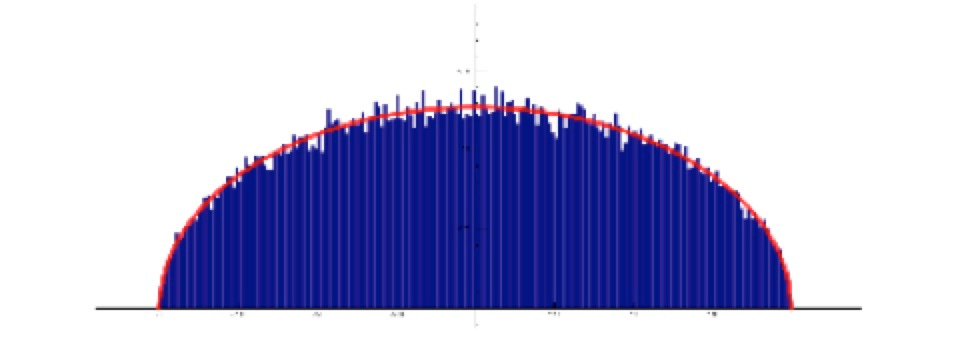
— here x and y are positive integers less than p, and the notation means that the difference between the two sides is a multiple of p. The Sato-Tate conjecture predicts qualitatively how the number of solutions varies as p varies. Reportedly Mikio Sato and John Tate arrived at the conjecture independently — Sato by studying data produced by computer and Tate by theoretical reasoning. The conjecture is now a theorem — I contributed to the solution — but even before it was proved it had inspired a series of more general conjectures, including the Katz-Sarnak conjectures relating (among other things) distributions of prime numbers to random matrix theory, which themselves have been supported by numerical data provided by computers.
The red curve is the Sato-Tate distribution that represents the theoretical number of solutions of an elliptic curve congruence as the prime p varies. The blue bars are a histogram calculated by computer by sampling a large set of primes.
The availability of rapid digital computation has even affected the norms of the field. In the 1950s and early 1960s, Y. Taniyama and G. Shimura formulated the Modularity Conjecture, whose solution was the essential step in Andrew Wiles's proof of Fermat's Last Theorem — a result that for some reason obsesses the formalizers. Later André Weil published the first statement of the conjecture in print, in a more precise form that was then successfully verified by computer in hundreds of cases, long before being proved finally by Breuil, Conrad, Diamond and Taylor. For Jean-Pierre Serre, one of the most influential mathematicians of the past century, Weil deserved (at least) equal credit with Taniyama and Shimura for the conjecture: the "importance [of Weil's version] comes from the fact that it made the conjecture checkable numerically" — meaning checkable by machine.
Mathematicians did not find the use of computers for rapid calculation at all controversial — no more than paper and pencil calculation, which extreme purists might consider an inappropriate substitute for pure thought. Nor did anyone object when computer algebra systems like Macsyma, Mathematica, Maple, and Sagemath were introduced, starting in the 1960s, to facilitate manipulation of complex symbolic expressions or to generate graphs like the one above. A few years ago my colleagues on the editorial board of Astérisque, a prestigious journal of the Société Mathématique de France, were happy to accept a monograph containing the instructions for implementing an algorithm for determining the set of unitary representations of a reductive Lie group. This problem, which first arose in the setting of quantum mechanics, is of fundamental importance for branches of mathematics ranging from mathematical physics to number theory. The earliest work on the problem gave solutions for the simplest groups, in the form of standard mathematical proofs. But the most experienced specialists — a group to which the authors of the Astérisque volume belong — gradually came to believe that there is no uniform solution that works for all groups.4 Thus their book provides those working in other areas with a means, to be carried out by the atlas software package, to solve the problem for any given group — assuming their computer has sufficient capacity for the group in question.
The reaction was quite different when Appel and Haken announced their computer-assisted proof of the Four Color Theorem. The theorem, conjectured in the 19th century, claims that any map can be colored with no more than four distinct colors in such a way that no two countries sharing a border have the same color. For more than 100 years the problem intrigued beginners, amateurs, and professional mathematicians alike. The question is equivalent to a statement about planar graphs, and the subject of graph theory, which has fundamental applications in computer science, was stimulated in part by attempts to prove and to generalize the Four Color Theorem. The Appel-Haken proof built on previous approaches to reduce the problem to a large but finite set of possible counterexamples. Eliminating the counterexamples by hand was (and remains) unfeasible, but a computer checked them one by one and completed the proof.
Or did it? Battle lines began to be drawn as soon as the Appel-Haken proof was announced, and have scarcely budged since. Disagreements about the status of the proof were so lively that it attracted unusual attention from sociologists and philosophers, who were quick to see it as a watershed moment for epistemology of science.5 Of course many mathematicians welcomed the new methods:
The members of what Harry Collins calls the core set, those mathematicians attempting a similar proof using similar computerized means, accepted the mechanized part of Appel and Haken’s analysis as almost certainly correct, and they focused their doubts on the complicated human reasoning involved. (MacKenzie, pp. 15-16)
But there was also widespread dissatisfaction with the absence of a traditional proof. The reaction of American mathematician Paul Halmos was more vivid than most but typical:
We are still far from having a good proof of the Four Color Theorem. . . . The present proof relies in effect on an Oracle, and I say down with Oracles! They are not mathematics.
Many mathematicians argued that the point of proving a theorem is less to establish its truth than to understand why it is true; thus Frank Bonsall wrote
if the solution involves computer verification of special cases . . . such a solution does not belong to mathematical science at all. . . . We cannot possibly achieve what I regard as the essential element of a proof—our own personal understanding—if part of the argument is hidden away in a box.
and the eminent Belgian mathematician Pierre Deligne reportedly told his colleague and compatriot David Ruelle, in response to a comment about the Four Color Theorem, that
ce qui l'intéressait personnellement c'étaient les résultats qu'il pouvait lui-même, et tout seul, comprendre dans leur intégralité. Cela exclut, dit-il, d'une part les résultats prouvés avec l'aide d'un ordinateur, d'autre part les résultats dont la … est tellement longue qu'elle dépasse les possibilités de vérification par un seul mathématicien.6
Naturally, there was also concern about the reliability of the computer system that verified the proof. Errors are frequent enough in human proofs, but they can in principle be detected by other humans. This is impossible with the Appel-Haken proof, that required more than 1000 hours of computer time. The issue of reliability came to the fore with the next major event in the history of computer-assisted proofs: Thomas Hales's determination of the most efficient way to pack spheres in 3-dimensional space, completed with his PhD student Samuel P. Feguson,. The problem is known as Kepler's conjecture, because it was mentioned by Kepler as early as 1611, making it perhaps the oldest unsolved problem that was still of interest to mathematicians when Hales announced his solution in 1998.
A pile of oranges in front of a grocery stand will almost certain be arranged as indicated in Figure •: each story is a hexagonal array with the oranges on the next story placed in the middle of each hexagon. Kepler's conjecture is roughly the statement that this is the arrangement that leaves the least empty space. As in the proof of the Four Color Theorem, Hales's strategy to prove the conjecture came down to reducing it to a finite series of computations, which were then checked by computer.
Hales submitted his proof to the prestigious Annals of Mathematics, published by Princeton University and the Institute for Advanced Study. What happened next, according to Hales, was unprecedented in the history of mathematics:7
After four full years, Gabor Fejes Toth, the chief referee, returned a report stating that he was 99% certain of the correctness of the proof, but that the team had been unable to completely certify the proof.
Robert MacPherson, editor of the Annals, wrote a report that states
“The news from the referees is bad, from my perspective. They have not been able to certify the correctness of the proof, and will not be able to certify it in the future, because they have run out of energy to devote to the problem. This is not what I had hoped for.”
The French text continues:
Comment se sortir de cette situation où des démonstrations semblent justes mais sont impossibles à vérifier ? Quand il est devenu clair que sa preuve ne pouvait pas être validée par le système habituel d’examen par les pairs (des humains), Thomas Hales a eu recours à la vérification formelle. Après une immersion rapide dans les techniques inventées par les informaticiens, le mathématicien a annoncé en 2003 la création du projet Flyspeck, avec l’objectif de réécrire sa preuve dans un langage symbolique pour produire une vérification mécanique. Il avait prévu que la formalisation prendrait vingt ans de travail, mais l’accueil de son projet a été si enthousiaste que l’équipe Flyspeck, qui comptait alors vingt-deux membres, a atteint son objectif dès 2014.
Thomas Hales n’a pas été le seul à s’intéresser sérieusement à la formalisation. En 2005, Georges Gonthier et Benjamin Werner, d’Inria, ont formalisé le théorème des quatre couleurs avec le système Coq. En 2007, l’équipe de Jeremy Avigad, de l’université Carnegie-Mellon, à Pittsburgh, a formalisé le théorème des nombres premiers en utilisant l’assistant de preuve Isabelle. Dans le cadre du projet Flyspeck, Thomas Hales a aussi formalisé le théorème de Jordan qui dit que, dans le plan, une courbe fermée simple sépare l’espace en deux parties, et dont la preuve étonnamment subtile avait résisté aux mathématiciens du xixe siècle pendant des décennies. Plus récemment, Thomas Hales s’est tourné vers Lean, l’assistant de preuve développé par Microsoft, qui est de plus en plus adopté sur le plan international, en particulier par le projet Xena, mené par le spécialiste de la théorie des nombres Kevin Buzzard, de l’Imperial College, à Londres.
La formalisation des preuves est désormais une branche reconnue des mathématiques. Pour les experts de ce domaine, l’objectif est surtout de rendre la formalisation facile d’accès pour intégrer sa pratique dans les usages courants du mathématicien.8
After that the text returns to the material I published here last August. There are also a sidebar on the mathematics of the Liquid Tensor Challenge and a shorter sidebar, written by Sean Bailly, on the DeepMind collaboration reported here, as well as two inserts on elliptic curves and on the Feigenbaum number.
My article was the cover story for the May issue of Pour la Science, which was published one month after a special issue entitled “How far will artificial intelligence go?” But look at the difference between the title of my article and the title on the cover.
This title — “The human soon outstripped by machines” — was originally proposed for my article, but I managed to convince the editors at Pour la Science to stick with the title that translates to the title of this week’s newsletter, and that doesn’t buy into the framework of humanity’s looming obsolescence. I can’t second-guess the editors, who must have figured that a title that hints at a clock ticking toward an imminent catastrophe would attract more readers. But mathematicians are not subject to market imperatives and have no excuse to suspend our critical faculties.
There is some overlap in the articles published by the two editions but they are not the same. According to (French) Wikipedia, “Les articles de fond sont rédigés par des chercheurs français ou adaptés d'articles parus dans le mensuel américain Scientific American, dont Pour la science est l’édition française.” My article appeared solely in the French publication.
As a journal of “vulgarisation” Pour la Science is allowed to oversimplify the history as well as the science for the sake of communication. I make no claims regarding the accuracy of the history or the relevance of the examples I chose. Professional historians are invited to send me their objections in private.
For example: when D = 1 it is finite, when D = 25 it is infinite. There are extensive tables — generated by computers, of course! — with information of this kind. Such tables confirm the BSD conjecture with high accuracy in many cases when it has not been proved. So of course every number theorist would be shocked to learn some day that the conjecture has been shown to be false, or to be undecidable in Gödel’s sense. Whether or not this extensive empirical evidence in favor of the conjecture justifies such an attitude with regard to the theoretical question that can only be answered by a proof of the conjecture is a matter that deserves more philosophical scrutiny. (Benacerraf’s Mathematical Truth is a classic treatment of related questions that has nothing to say about conjectures, however.)
Most mathematical problems are like this. The famous 10th problem on the list proposed by David Hilbert in 1900, asking for an algorithm to solve all diophanine equations, the basic problem in number theory, was proved impossible in the middle of the last century by Martin Davis, Yuri Matiyasevich, Hilary Putnam and Julia Robinson. Because the theory of reductive groups has such a rigid structure, it was hoped that the problem of classifying unitary representations would have a closed form solution, but now most experts have stopped looking.
The best account of the controversy, covering the period before 2000, is contained in Donald MacKenzie's book Mechanizing Proof, which is my source for much of the following.
David Ruelle, Hasard et chaos, p. 12. Very few mathematicians have ever enjoyed Deligne's powers of understanding. It can be argued that the dependence of mathematics on the understanding as well as the imagination of exceptional individuals like Deligne and Scholze is no less problematic than its potential dependence on machines. This argument is beyond the scope of this article.
https://code.google.com/archive/p/flyspeck/wikis/FlyspeckFactSheet.wiki
The copyright for this text — written by me only in French and corrected by Sean Bailly — belongs to Pour la Science. I think (and hope) this qualifies as fair use.