Does mathematics "progress"?
And if it does, what does technology have to do with it?

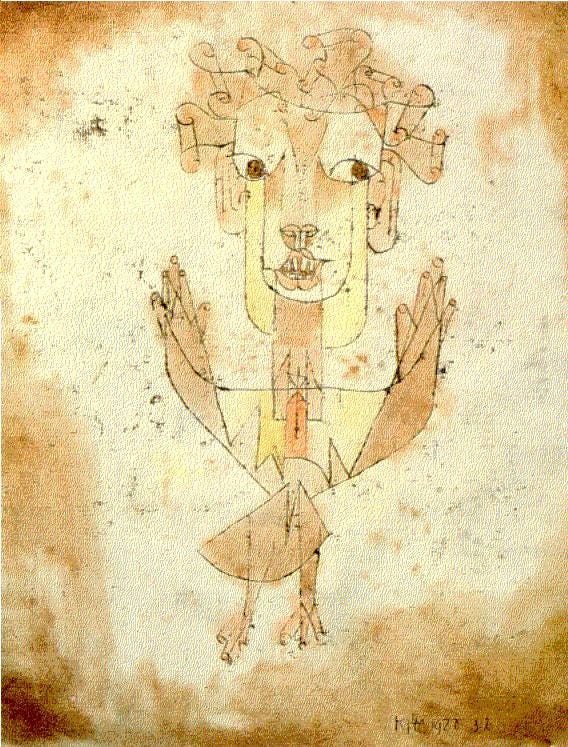
Paul Klee’s Angelus Novus, pictured above, is perhaps known primarily as the image that inspired these lines by Walter Benjamin:
…a storm is blowing in from Paradise; it has got caught in his wings with such a violence that the angel can no longer close them. The storm irresistibly propels him into the future to which his back is turned, while the pile of debris before him grows skyward. This storm is what we call progress. [my emphasis] (On the Concept of History)
Alternatively, in Terry Eagleton's reading:
History is hurtling out of control, and revolution is necessary if we are to get a decent night’s sleep.
Or, as Mme. Cottard observed in Proust’s A l'ombre des jeunes filles en fleurs:
Il me semble que je n'aimerais pas avoir le téléphone à domicile. Le premier amusement passé, cela doit être un vrai casse-tête.1
This is an expanded and slightly revised version of a post that first appeared on May 5, 2021 on the blog mathematicswithoutapologies.wordpress.com. (And that blog post is also where readers are invited to comment on this revised version.) I will periodically be revising old blog posts and recycling them on this newsletter. The point of today’s entry is to address the usually tacit intertwined assumptions that technology is the source of (or is the factor primarily responsible for) something called “progress,” that technological “progress” is a good thing, that it is moreover inevitable because it is governed by its own logic, and that all of this means that mathematics hungers for technological progress. Like every other notion, that of “progress” is not self-evident; it has a history, and understanding this history is indispensable if we want to evaluate claims about the inevitability or the desirability of mechanization of mathematics on the grounds that it would constitute “progress.” I am not a historian so I can only point to the need to understand the relevant history, not to satisfy this need.
Mechanization of mathematics, at least in certain aspects, has been welcomed as "progress," notably in a comment by Kevin Buzzard on my blog:
I think of it as progress. I multiply numbers together on my phone instead on a piece of paper. It’s all the same thing. It makes us faster. It makes us better.
Most readers of my blog, I suspect, will embrace the "progressive" label, if the alternative is what is being promoted on the Killing Obama's Radical Progressive Agenda Facebook page. Nevertheless, as the image below vividly reminds us, the notion of "progress" in its current usage is so thoroughly entwined with technological determinism, European colonialism, genocide, and environmental devastation, that it is a struggle to find an interpretation of the word, applicable to mathematics, whose connotations are unequivocally positive.

The OED traces the first use of the word, in its second definition, the (originally metaphorical) sense of
Advancement to a further or higher stage, or to further or higher stages successively; growth; development, usually to a better state or condition; improvement…
to 1457 in the Acts of Parliament of Scotland, in the sentence
Sen Gode..hes send oure souerane lorde sik progres and prosperite, that [etc.].
The word's current use evolved from the mid-18th through 19th centuries, from the Enlightenment through the Industrial Revolution. The OED quotes Benjamin Franklin using the word in 1780. In 1794 the Marquis de Condorcet wrote his Sketch for a Historical Picture of the Progress of the Human Mind, "perhaps the most influential formulation of the idea of progress ever written" according to Wikipedia, while hiding on the "rue des Fossoyeurs" (the present-day Rue Servandoni) in Paris from the warrant for his arrest issued by the Convention. (By dying in prison, Condorcet escaped the guillotine, a fitting “symbol of the penal, technological and humanitarian progress inspired by the Enlightenment" according to the Open University website.)
In the 19th century "progress" was a watchword for thinkers as diverse as Hegel, Comte, Marx and Engels ("entire sections of the ruling class are, by the advance of industry, precipitated into the proletariat [… and] also supply the proletariat with fresh elements of enlightenment and progress"), Darwin, and Herbert Spencer ("the civilized man departs more widely from the general type of the placental mammalia than do the lower human races").
Perhaps the most evocative tribute to technological progress and its ability to shape society," writes Merritt Roe Smith, "is John Gast's 1872 oil painting entitled 'Westward ho' or 'American Progress,' pictured above. Smith continues:
In his commission, the patron publicist George Crofutt instructed Gast to paint a ''beautiful and charming female . . . floating westward through the air, bearing on her forehead the 'Star of Empire."'"She has left the cities of the East far behind," Crofutt imagined, "and still her course is westward. In her right hand, she carries a book—common school—the emblem of education and the testimonial of our national enlightenment, while with the left hand she unfolds and stretches the slender wires of the telegraph, that are to flash intelligence throughout the land. . . . Fleeing from 'Progress' are the Indians, buffalo, wild horses, bears and other game, moving westward—ever westward. The Indians . . . turn their despairing faces toward the setting sun, as they flee from the presence of wondrous vision. The 'Star' is too much for them."
Wikipedia's caption draws together the themes of technological determinism, settler colonialism, and Darwinism both biological and social (through allusions to extinction and extermination) as they are illustrated in this painting:
This painting shows "Manifest Destiny" (the belief that the United States should expand from the Atlantic to the Pacific Ocean). In 1872 artist John Gast painted a popular scene of people moving west that captured the view of Americans at the time. Called "Spirit of the Frontier" and widely distributed as an engraving portrayed settlers moving west, guided and protected by Columbia (who represents America and is dressed in a Roman toga to represent classical republicanism) and aided by technology (railways, telegraph), driving Native Americans and bison into obscurity. The technology shown in the picture is used to represent the outburst of innovation and invention of modern technology. It is also important to note that Columbia is bringing the "light" as witnessed on the eastern side of the painting as she travels towards the "darkened" west.
Gast's painting is one illustration of a principle that was generally accepted by European colonizers, including the American settlers, and given clear expression by the German Rudolf Cronau in 1896:
The current inequality of the races is an indubitable fact. Under equally favorable climatic and land conditions the higher race always displaces the lower, i.e., contact with the culture of the higher race is a fatal poison for the lower race and kills them…. [American Indians] naturally succumb in the struggle, its race vanishes and civilization strides across their corpses…. Therein lies once again the great doctrine, that the evolution of humanity and of the individual nations progresses, not through moral principles, but rather by dint of the right of the stronger.
Rudolf Cronau, in Friedrich Hellwald, Kulturgeschichte in ihrer natürlichen Entwickelung, 4th ed., 4 vols. (Leipzig: Friesenhahn, 1896 ), IV: 615-16
Other colonial powers used the notion of progress in similar ways. Gast's painting is well-known but I only became aware of it a few months ago, when I watched Raoul Peck's extraordinary four-part documentary Exterminate all the Brutes! Peck's title is a quotation from Conrad's character Kurtz — "an emissary of pity and science and progress, and devil knows what else" — in Heart of Darkness. "By the simple exercise of our will we can exert a power for good practically unbounded," Kurtz had written, a few lines before arriving at the words that served as Peck's title. This was the intellectual matrix in which Hitler formed his world view. The word "progress," in expressions like "human progress" or "progress of mankind," appears dozens of times in Mein Kampf. For example:
Not through [the Jew] does any progress of mankind occur.
Mein Kampf, Chapter XI.
Now that Godwin's law has been reconfirmed, possibly for the first but certainly not for the last time, in connection with mechanization of mathematics, I can quickly come to the point of this post, which is to draw attention to the questions that are not being asked when the desirability or feasibility of mechanization of mathematics is under debate. Arundhati Roy asked one such question in her first non-fiction book, about the Narmada Dam project:
How can you measure progress if you don't know what it costs and who has paid for it?
Arundhati Roy, The Cost of Living, Random House of Canada, 1999
Twenty years after the book's publication, Tina Stevens and Stuart Newman defended the precautionary principle as protection from the "hidden agendas of BioTechnical science" —
Precaution does not derail progress; rather, it affords us the time we need to ensure we progress in socially, economically, and environmentally just ways.
Tina Stevens and Stuart Newman, Biotech Juggernaut, Routledge, 2019
and Roy is still writing about the dam, which has submerged at least 178 villages in Madhya Pradesh:
Of course, you cannot see the river valley civilisation that lies destroyed, submerged in the depths of the vast reservoir, or hear the stories of the people who waged one of the most beautiful, profound struggles the world has ever known – not just against that one dam, but against the accepted ideas of what constitutes civilisation, happiness and progress.
Arundhati Roy, Guardian, April 28, 2021
Most of the mathematicians and philosophers who promote mechanization are perfectly candid about their agendas, and cannot be suspected of genocidal tendencies. But the potential implications of the widespread adoption of technological solutions to perceived mathematical problems — "what it [will] cost… and who [will pay] for it," not to mention the question of who stands to benefit — are simply not being acknowledged.
Technological progress, in the words of its advocates
Progress as conceived by tech prophets, and by the promoters of mathematical mechanization, preserves only a distant echo of the age of empire. There are still worlds to conquer, only not on this planet. Mars, a popular choice, is name-checked in a blog post by Balaji Srinivasan that explicitly calls on "people with scientific and technical backgrounds" to "evangelize technological progress" in the name of eternal life:
…insofar as reducing scarcity is acknowledged to be the proximate purpose of technology, eliminating the main source of scarcity – namely mortality – is the ultimate purpose of technology.
But Srinivasan is mainly known as an investor in virtual counterparts to this world. Fortune calls him a top crypto prognosticator. Continuity with 19th century imperialist antecedents comes through in his ten-point defense of cryptocurrency, the foundation of a "new [international] code-based order," as the cure for the defects of what he calls "the old civilizational order" — what you and I know as democracy.
A yearning for immortality is fairly widespread in the tech universe, but scorn for democracy and the associated regulation is pervasive, on the principle that progress is driven by nonstop disruption of vestigial institutions like democratic oversight. Insofar as this outlook has an ethical compass, it is summarized in this sentence, quoted approvingly by Srinivasan:
the “can't be evil” internet protects [freedom] through code and mathematics.
The ethos of automated proof verification converges with blockchain evangelism in their common distrust of "fallible" social processes [see below!] of validation and their preference for what can be pinned down and immobilized in "code and mathematics." The code that validates itself with the strict minimum of human intervention is recognizable as a contemporary version of Leibniz's infallible characteristica universalis, initially proposed as a solution to political conflict, now being revived as a way of dispensing with politics altogether. Leibniz was writing in a continent in a constant state of war. In the 21st century war is world-wide, and Srinivasan displays more than a hint of Leibnizian optimism when he writes that
cryptocurrencies offer the possibility of bringing us together on the basis of tangible, quantifiable economic alignment. It is now possible for an Israeli and a Palestinian, a Chinese citizen and a Japanese citizen, or a Democrat and a Republican, to all agree on the state of the Bitcoin blockchain. Regardless of your political views or your geography, everyone in the same crypto network prospers or fails together.
You may or may not agree with Leibniz and Srinivasan that "code and mathematics" can protect peace as well as freedom, but I would hope that upon reflection you agree that self-validating mathematics satisfies few of the goals that drive the community of mathematicians.
Mathematics as goal-directed
Promoters of the notion of mathematical progress echo the 18th and 19th century thinkers who conceived of the whole of history, in increasingly racist and colonialist terms, as movement towards an outcome or conclusion. Other thinkers in other times and places have seen history as cyclical or aimless or as a kind of "punctuated equilibrium." If we want to allow for these differing views of history we can scrap the OED's second definition and return to its first definition:
Progression or advancement through a process, a sequence of events, a period of time, etc.; movement towards an outcome or conclusion.
This directly conveys the meaning of the original Latin progressus, from the verb gradior (advance, go), derived (according to Wiktionary) from Proto-Indo-European *gʰredʰ- (“to walk, go”), all of which is innocent of value judgment and rescues the word from its unfortunate associations.
Unlike history, on the other hand, mathematics seems unquestionably to be a goal-directed activity. Then "progress" in mathematics would simply be "movement towards" the goal of that activity. Maybe the debate over mechanizing mathematics will then be settled one way or the other as soon as we determine whether or not it represents "movement towards" that goal. Or maybe not. It's possible and even likely that mathematics has multiple goals, that some of these goals may be strictly incompatible, and that the rapid development of mechanized mathematics will serve the ultimately salutary purpose of exacerbating the tensions among conflicting goals.
But how can we identify the goal, or goals, of mathematical activity? Imre Lakatos seems to provide an answer in his distinction between scientific research programs that are "progressive" and "degenerating." To say that the goal of mathematics is "progress" is uncomfortably circular, but Lakatos is more specific than that:
in a progressive research programme, theory leads to the discovery of hitherto unknown novel facts. (Lakatos, The Methodology of Scientific Research Programmes, p. 5)
Or to quote the online Stanford Encyclopedia entry on Lakatos:
What is it for a research programme to be progressive? It must meet two conditions. Firstly it must be theoretically progressive. That is, each new theory in the sequence must have excess empirical content over its predecessor; it must predict novel and hitherto unexpected facts (FMSRP: 33). Secondly it must be empirically progressive. Some of that novel content has to be corroborated, that is, some of the new “facts” that the theory predicts must turn out to be true.
("Imre Lakatos", Stanford Encyclopedia of Philosophy)
This is a good way to begin our search for goals. Natural science has the edge over mathematics in that all the "novel and hitherto unexpected facts" predicted by its theories have something to do with the world, and thus have a good prima facie claim to being interesting. We can argue whether the word "facts" is helpful as a way a way of talking about mathematics, but its very exuberance in making predictions that interest no one is a reminder that novelty and unexpectedness are not sufficient to qualify a (corroborated) mathematical prediction as progress.
With this in mind, we can begin to evaluate claims like this one:
We welcome the prospect of formalizing mathematics. In our view, the traditional social process is an anachronism to be swept away by formalization, just as empiricism replaced a similar ‘social process.’
(John Harrison, "Formal Proof—Theory and Practice," Notices of the AMS, 2008, p. 1400)
Let's not get hung up on vocabulary: the word "anachronism" here clearly signifies the ailment for which progress is the cure. Sweeping away the anachronism — and it's worth pausing to contemplate the implicit violence of this rhetoric — must have something to do with the goals of mathematical activity, because Harrison's article was published in the main forum of opinion of our most influential professional society, but what it is can only be surmised from the body of Harrison's text. Following Lakatos's lead while reading the text, we can ask: does formalization lead to theoretical progress, to empirical progress (whatever that might mean), and — most importantly — to a third sort of progress that Lakatos omitted because mathematics is not a natural science?
I will eventually take this up in a subsequent post, but you won't be surprised to learn that after subjecting the argument to analysis I conclude that I don't recognize as mine the goals Harrison, principal engineer at Intel Corporation, attributes to mathematics in this article (which I quoted in an earlier newsletter and which I anticipate quoting again in the future; Harrison has elsewhere issued disclaimers but he is hardly the only person who writes this sort of thing.) I will argue instead, possibly starting in two weeks, that the “social process” itself constitutes the primary goal of mathematics, in the same way that the quotation from Meredith Broussard near the end of this entry asserts that humans, the participants in any social process, are the point. Note that Broussard saw no need to defend nor even to explain her assertion.
I want to conclude with two quotations from a notorious article of the composer Milton Babbitt, published in 1958 in High Fidelity magazine and entitled "Who Cares If You Listen?" (The year 1958 also saw the publication of the article "Heuristic Problem Solving… " by Newell and Simon, that first promised an automated proof of "an important new mathematical theorem" — within ten years, as usual; I have already referred to this article in a previous newsletter and I hope to carry out a close reading in the future.) Babbitt had studied mathematics and was on the Princeton mathematics faculty between 1943 and 1945, before moving permanently to the music department, where 25 years later, when I was an undergraduate, serialism had been established as such an unshakeable dogma, largely (so I was told) because of Babbitt's domination of the department, that it was taken for granted that “progress” in music could only be serial.
Imagine, if you can, a layman chancing upon a lecture on "Pointwise Periodic Homeomorphisms." At the conclusion, he announces: "I didn't like it."
The layman’s objections are ruled out of order and "the development of mathematics is left undisturbed." By the same reasoning, the "composer of … 'serious,' 'advanced,' contemporary music" has no reason to care whether or not "You" listen. Babbitt uses the word "development" rather than "progress" but the intention is the same, as is the use of the word "evolve" in the following excerpt:
Granting to music the position accorded other arts and sciences promises the sole substantial means of survival for the music I have been describing. Admittedly, if this music is not supported, the whistling repertory of the man in the street will be little affected, the concert-going activity of the conspicuous consumer of musical culture will be little disturbed. But music will cease to evolve, and, in that important sense, will cease to live.
Together with Clement Greenberg's 1939 essay "Avant-Garde and Kitsch," published in the Partisan Review (during its Trotskyist period), Babbitt's piece usefully brackets what you might call the high highbrow period of cultural snobbism in the United States. Both "Avant-Garde and Kitsch" and "Who Cares If You Listen?" are deemed important enough to merit their own Wikipedia pages. It's generally assumed that the "You" of Babbitt's title is the consumer of Greenberg's "Kitsch" and that the the healthy indifference of mathematicians to the opinion expressed by the "layman" in the above thought-experiment serves as Babbitt’s model for the "Who Cares?" attitude. Greenberg's pre-war essay is political in a way that Babbitt's Cold War article is not, but the two articles share a concern for something like "progress" in the arts; as Greenberg puts it,
the avant-garde moves…. And this, precisely, is what justifies the avant-garde's methods and makes them necessary. The necessity lies in the fact that by no other means is it possible today to create art and literature of a high order.
Neither Babbitt's "evolution" nor Greenberg's "movement" (which echoes the first OED definition of "progress") "leads to the discovery of hitherto unknown facts" as Lakatos understood them. But the way we talk about "progress" as understood in Kevin Buzzard's comment — the kind that makes us "faster" and "better" — must have developed through interaction with its surrogates in the mid-20th century high culture sphere. One of our tasks — going forward! — will be to retrieve hints of this dialogue.
In C. Scott Moncrieff’s (exceedingly loose) translation: “I don't think I should like to have the telephone in my establishment. Once the first excitement is over, it must be a perfect racket going on all the time.” Thanks to Amadou Bah for pointing out my incorrect attribution of this line to Mme. Bontemps.