Cantor's paradise is a place where nothing ever happens
Can mathematics be done by machine? II: Notes for a Columbia course with Gayatri Chakravorty Spivak and special guest Kevin Buzzard, continued
This is the continuation of the installment published four weeks ago. The two parts consist of the notes I prepared for the November 4, 2020 session of the course, entitled “Mathematics and the Humanities,” that I taught with Gayatri Chakravorty Spivak. Kevin Buzzard was the guest. For the most part the notes have not been amended, but I have added some additional material to explain allusions to earlier sessions of the course.
Mechanical vs human reasoning: an old controversy
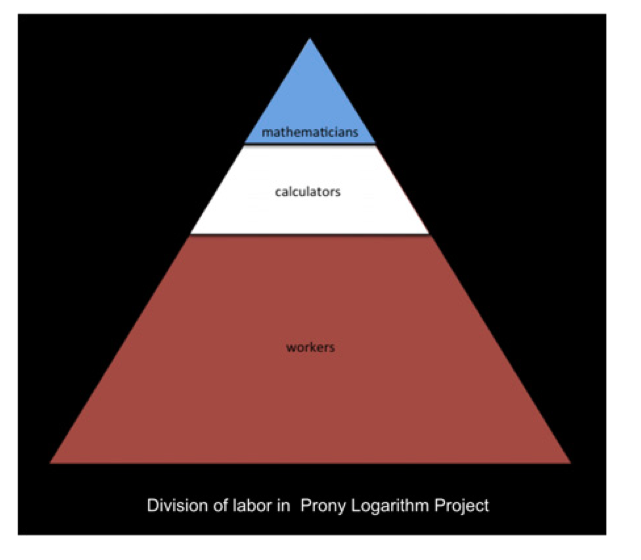
In the 1820s Gaspard Riche de Prony, inspired by Adam Smith's account of the division of labor in pin making (itself inspired by an article in the Encyclopédie), created a pyramid of logarithm calculators (to 14 decimal places), divided into three categories: mathematicians "of distinction" at the top, workers at the bottom who actually did the arithmetic, and "algebraists" in the middle to translate the mathematical rules into mechanical algorithms for the unskilled (see Figure 1 above).
Lorraine Daston reports, in “Calculation and the Division of Labor, 1750-1950,” that Prony's method in turn “greatly impressed” Charles Babbage:
Human intelligence sunk to the mechanical level, kindling the idea of machine intelligence. (Daston , p. 11)
Daston calls the middle stratum "analytical intelligence" and traces the degradation of the reputation of calculating skill as versions of this division of labor was adopted during the 19th century.
In a passage that Babbage was to repeat like a refrain, Prony marveled that the stupidest laborers made the fewest errors in their endless rows of additions and subtractions: “I noted that the sheets with the fewest errors came particularly from those who had the most limited intelligence, [who had] an automatic existence, so to speak.” (Daston, p. 17)
Plans to mechanize mathematical research can be expected to have the same effect: which rung do today's "mathematicians of distinction" expect to occupy?
We will return to this question in the upcoming essays on Luddism.
The intellectual bias of our time
Already in 1829, Thomas Carlyle could complain of "the intellectual bias of our time," that "what cannot be investigated and understood mechanically, cannot be investigated and understood at all" and that "Intellect, the power man has of knowing and believing, is now nearly synonymous with Logic, or the mere power of arranging and communicating." But even mathematicians were not ready to mechanize:
The “cold algebraists,” reduced the once-noble science of mathematics to mere mechanical calculation, without any deeper meaning. While Fergola “sees God behind the circle and the triangle,” these atheists “see only the nothingness behind their formulas.” ...
Moreover, for the anti-algebraists of Naples, “certainty” was on the side of intuition, not mechanical calculation.
(Massimo Mazzotti, writing about mathematics in Naples in the 1830s)
Analysis functioned as a shortcut; a sort of machinery of symbols that one need only “to arrange on paper, following certain very simple rules, in order to arrive infallibly at new truths.” The very efficiency of the mechanical process, which obscured the route by which it achieved its results, rendered it suspect to mathematicians who believed that valid reasoning demanded clear and distinct ideas. ... The metaphor of the blind machine of analysis, which cranks out its results magically and mysteriously, recurs throughout the writings of [French] synthetic geometers.
Lorraine Daston, on mathematics in Paris in the early 19th century
I am also interested in the anthropomorphic language that many automated theorem proving practitioners used to talk about what kind of contributions they thought computers would be able to make to mathematics - some calling them future "mentors," "colleagues," and "co-workers," others comparing them to "high school students," or "apprentices," and still others calling them "assistants," "slaves," and "servants" - it seems to me that this anthropomorphic language has to do with what human faculties researchers expected would be automatable, and certain valuations and devaluations of mathematical labor. This, too, situates computing in the longer history of labor, human computing, and automation!
Stephanie Dick, private communication about her work in progress
From Burroughs to Burroughs
What was optimal for human minds was not optimal for machines … at the level of the procedures required to mesh human and machines in long sequences of calculation, whether in the offices of the Nautical Almanac or the French Railways, tasks previously conceived holistically and executed by one calculator had to be analyzed into their smallest component parts, rigidly sequenced, and apportioned to the human or mechanical calculator able to execute that step most efficiently — where efficiently meant not better or even faster but cheaper.
In a sense, the analytical intelligence demanded by human-machine production lines for calculations was no different than the adaptations required by any mechanized manufacture… Daston, p. 28
[The] junk merchant does not sell his product to the consumer, he sells the consumer to his product. He does not improve and simplify his merchandise. He degrades and simplifies the client. W. Burroughs, Naked Lunch
[Cantor's paradise] is a place where nothing really happens
Harris writes that to computers, every “step” is the same. Computers cannot, unless directed by a person, identify those “steps” in a proof that contain what he calls the key - the particular insight that captures the why rather than the that of a theorem’s truth … some “key” or “main” or “crucial” or “fundamental” or “essential” insight that “hints that mathematical arguments admit not only the linear reading that conforms to logical deduction but also a topographical reading that more closely imitates the process of conception.” He cites David Byrne’s … “heaven is a place where nothing ever happens” to introduce the world of the computer where all steps are created equal, all inferences are merely steps, and computers cannot show people what “key” insight grounds the truth or reveals the why of a mathematical theorem.
The very possibility of automated theorem-proving, according to Harris, is predicated on the belief that “nothing really happens when a theorem is proved.”
(Stephanie Dick, 2015 Harvard Dissertation)
Algorithms and dreams
The next four quotations are taken from my essay Do Androids Prove Theorems in Their Sleep? The starting point for that essay is the story with which Robert Thomason introduced the article “Higher algebraic K-theory of schemes and of derived categories”1 that he cosigned with his friend Thomas Trobaugh. Thomason was one of his generation’s most influential specialists in algebraic K-theory2 of his generation, and the article with Trobaugh is considered one of his most important contributions; it has been cited 443 times (as of today’s date), which is more than three times as many citations as his next most cited article.
It is appropriate that I am writing these lines on Hallowe’en 2021, because the Thomason collaboration with Trobaugh was peculiar in at least three respects. First of all, Trobaugh was not a mathematician; next, Trobaugh had been dead for three months at the time of the collaboration; and finally — and most importantly for the purposes of my essay — the collaboration took place in a dream. Here is Thomason’s account of the incident, from p. 249 of the article:
The first author must state that his coauthor and close friend, Tom Trobaugh, quite intelligent, singularly original, and inordinately generous, killed himself consequent to endogenous depression. Ninety-four days later, in my dream, Tom's simulacrum remarked, "The direct limit characterization of perfect complexes shows that they extend, just as one extends a coherent sheaf." Awaking with a start, I knew this idea had to be wrong, since some perfect complexes have a non-vanishing K_0 obstruction to extension. I had worked on this problem for 3 years, and saw this approach to be hopeless. But Tom's simulacrum had been so insistent, I knew he wouldn't let me sleep undisturbed until I had worked out the argument and could point to the gap. This work quickly led to the key results of this paper. To Tom, I could have explained why he must be listed as a coauthor.
I am aware of no other remotely similar collaboration in the entire mathematical literature, and the editors of the volume in which the article appeared must be commended for their willingness to accept Trobaugh’s name as coauthor. Thomason himself died suddenly of diabetic shock at age 43, five years after the publication of his article with Trobaugh. I was therefore never able to ask him whether or not my essay was faithful to the circumstances of his article’s creation.
The central conceit of my essay was a narrative analysis of Trobaugh’s contribution to the collaboration, which was itself a way of asking whether a mechanical mathematician — called an android in my text — could ever create, or would ever want to create, a similar narrative structure.
…the typical strategy for automated theorem proving is a sophisticated version of the infinite-monkey scenario, with more or less intelligent guidance provided by the programmers but minus the monkeys. You begin with a collection of axioms defining the theory and add the negation of the theorem you want to prove. The program then applies logically valid transformations, possibly according to a predefined search strategy, until it arrives at a contradiction. … Another strategy Beeson discusses is quantifier elimination … What might be called recursive simplification includes both strategies mentioned above. It also underlies the principle of robot vacuum cleaner function, the task being completed recursively with the result guaranteed probabilistically. As far as I can tell, there is no key idea in either case. Trobaugh’s intuition, by contrast, is nothing but a key idea. But I do not know how to characterize Trobaugh’s intuition intrinsically, to show how it differs from the principles underlying the search strategies mentioned above.
(Beeson is Michael Beeson, author of an article entitled The Mechanization of Mathematics, a chapter in M. Teuscher's book Alan Turing: Life and Legacy of a Great Thinker. I consulted Beeson’s article extensively in writing my essay.)
Mathematics and narrative, 1
The android needs no semantics, by definition. The mathematician understands nothing without semantics. The ghost opens with a proposition about perfect complexes. One challenge in this article is to explain how this fits into the narrative without stopping to say what the terminology means. …
To detect a narrative structure in a mathematical text, first look at the verbs. Apart from the verbs built into the formal language (“implies,” “contains” in the sense of set-theoretic inclusion, and the like), nothing in a logical formula need be construed as a verb in order to be understood, and an automatic theorem prover can dispense with verbs entirely. One may therefore find it surprising that verbs and verb constructions, including transitive verbs of implied action, are pervasive in human mathematics. Trobaugh’s ghost’s single sentence consists of eighteen words, two of which are transitive verbs (shows, extends), one an intransitive verb (extends again); there is also a noun built on a transitive verb with pronounced literary associations (characterization).
Mathematics and narrative, 2
The word narrative lends itself to two misunderstandings. What for want of a better term I might call the “postmodern” misinterpretation is associated with the principle that “everything is narrative,” so that mathematics as well would be “only” a collection of stories (and more or less any stories would do). The symmetric misunderstanding might be called “Platonist” and assumes a narrative has to be about something and that this “real” something is what should really focus our attention. The two misunderstandings join in an unhappy antinomy, along the lines that, yes, there is something, but we can only understand it by telling stories about it. The alternative I am exploring is that the mathematics is the narrative, that a logical argument of the sort an android can put together only deserves to be called mathematics when it can be inserted into a narrative. But this is just the point I suspect is impossible to get across to androids.
Can mechanical mathematics be about something?
Can we even say what human mathematics is about?
The Thomason-Trobaugh article is a contribution to the branch of mathematics known as K-theory, specifically algebraic K-theory. The name used to designate this branch of mathematics has two parts, each of which poses its own problems. The insider sees mathematics as a congeries of semi-autonomous subjects called “theories”—number theory, set theory, potential theory. The word was first used to delineate a branch of mathematics no later than 1798… In the examples given above the construction points to a discipline concerned with numbers, sets, and potentials, respectively; the word theory functions as a suffix, like -ology. But then what on earth could K-theory be about? Analyzing how the term is used, I am led to the tentative conclusion that it refers to the branch of mathematics concerned with objects that can be legitimately, or systematically, designated by the letter K. … I do not know how to answer the very interesting question whether the shape of K-theory, long since a recognized branch of mathematics with its own journals … and an attractive two-volume Handbook, was in some sense determined by its name.
"Theorems for a Price"
Doron Zeilberger has proposed a radical alternative to automated proof verification, where the value of a mathematical statement is literally determined by the market.
Although there will always be a small group of "rigorous" old-style mathematicians …they may be viewed by future mainstream mathematicians as a fringe sect of harmless eccentrics. … In the future not all mathematicians will care about absolute certainty, since there will be so many exciting new facts to discover.… This will happen after a transitory age of semi-rigorous mathematics in which identities (and perhaps other kinds of theorems) will carry price tags.
… I can envision an abstract of a paper, c. 2100, that reads, "We show in a certain precise sense that the Goldbach conjecture is true with probability larger than 0.99999 and that its complete truth could be determined with a budget of $10 billion.
(Doron Zeilberger, 1993)
Conjecture (Christian Goldbach, 1742): Every even number greater than 2 is the sum of two prime numbers.
4 = 2+2, 6 = 3+3, 8 = 3+5, 10 = 3+7, 12 = 5+7, 14 = 7 + 7, 16 = 11+5,
18 = 11+7, 20 = 17+3, 22 = 17+5, 24 = 11+13, 26 = 13+13, 28 = 23+5…
This is known for all even numbers less than 4000000000000000000.
(See Uncle Petros and the Goldbach Conjecture by A. Doxiadis).
Ternary version: Every odd number n greater than 5 is the sum of three prime numbers. This was proved for very large n (starting with Vinogradov) and then for all n by Harold Helfgott in 2013.
in P. Cartier et al., eds, The Grothendieck Festschrift Volume III, Boston: Birkhâuser (1990) 247-429.
K-theory is one of the most challenging specialties to explain to someone who doesn’t already know what it is. My attempt to do so is contained in the paragraph under the heading “Can mechanical mathematics be about something”? See also the Wikipedia article on K-theory.